题目内容
1. 如图所示的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线.以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点,则抛物线的解析式是y=-$\frac{1}{9}$x2+$\frac{4}{3}$x.
如图所示的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线.以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点,则抛物线的解析式是y=-$\frac{1}{9}$x2+$\frac{4}{3}$x.
分析 根据题意可知抛物线经过点(0,0)、(12,0)、(6,4),然后利用待定系数法求解即可.
解答 解:设抛物线的解析式为y=ax(x-12),将点(6,4)代入得:-36a=4.
解得:a=-$\frac{1}{9}$.
∴抛物线的解析式为y=-$\frac{1}{9}$x2+$\frac{4}{3}$x.
故答案为:y=-$\frac{1}{9}$x2+$\frac{4}{3}$x.
点评 本题主要考查的是二次函数的应用,根据图形确定出抛物线经过点的坐标是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
11.下列图形是正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
13. 兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进20m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )
兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进20m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )
 兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进20m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )
兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进20m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )| A. | (10$\sqrt{3}$+2)m | B. | (20$\sqrt{3}$+2)m | C. | (5$\sqrt{3}$+2)m | D. | (15$\sqrt{3}$+2)m |
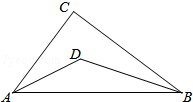 如图,在△ACB中,∠C=90°,∠CAB与∠CBA的角平分线交于点D,AC=3,BC=4,AB=5,则点D到AB的距离为1,则S△ABC=6.
如图,在△ACB中,∠C=90°,∠CAB与∠CBA的角平分线交于点D,AC=3,BC=4,AB=5,则点D到AB的距离为1,则S△ABC=6. 已知数a,b,c在数轴上的位置如图所示,试化简|a-b|+|a+b+c|-|c-b|.
已知数a,b,c在数轴上的位置如图所示,试化简|a-b|+|a+b+c|-|c-b|.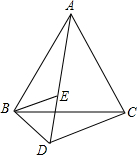 如图,已知△ABC和△BED都是等边三角形,且A、E、D在一条直线上,且DC=4,BD=2,求AD的长度?
如图,已知△ABC和△BED都是等边三角形,且A、E、D在一条直线上,且DC=4,BD=2,求AD的长度? 如图所示,DE是△ABC的中位线,DE=3,则BC=6.
如图所示,DE是△ABC的中位线,DE=3,则BC=6.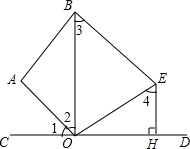 如图,已知∠1=∠2,OE⊥OA于点O,EH⊥CD于点H,∠3=∠4.求证:BE∥AO.
如图,已知∠1=∠2,OE⊥OA于点O,EH⊥CD于点H,∠3=∠4.求证:BE∥AO.