题目内容
20.解下列方程:(1)x2-10x+25=7;
(2)x2-14x=8;
(3)x2+3x=1;
(4)x2+2x+2=8x+4.
分析 (1)利用配方法得到(x-5)2=7,然后利用直接开平方法解方程;
(2)利用配方法解方程;
(3)利用求根公式法解方程;
(4)先把方程整理为一般式,然后利用配方法解方程.
解答 解:(1)(x-5)2=7,
x-5=±$\sqrt{7}$,
所以x1=5+$\sqrt{7}$,x2=5-$\sqrt{7}$;
(2)x2-14x+49=57,
(x-7)2=57,
x-7=±$\sqrt{57}$,
所以x1=7+$\sqrt{57}$,x2=7-$\sqrt{57}$;
(3)x2+3x-1=0,
△=32-4×1×(-1)=13,
x=$\frac{-3±\sqrt{13}}{2×1}$
所以x1=$\frac{-3+\sqrt{13}}{2}$,x2=$\frac{-3-\sqrt{13}}{2}$;
(4)x2-6x=2,
x2-6x+9=11,
(x-3)2=11,
x-3=±$\sqrt{11}$,
所以x1=3+,x2=3-$\sqrt{11}$.
点评 本题考查了解一元二次方程-因式分解法:就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法和公式法解一元二次方程.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,点P在线段CD上,且AD=2DB,∠APB=135°
如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,点P在线段CD上,且AD=2DB,∠APB=135°



 如图,有一个水池,其中CD为$\frac{5}{3}$m,池中央垂直长了一根芦苇,露出水面的部分高$\frac{1}{3}$m,把芦苇的顶端引到岸边,苇顶和岸边水面刚好齐平,求水深和芦苇的高度.
如图,有一个水池,其中CD为$\frac{5}{3}$m,池中央垂直长了一根芦苇,露出水面的部分高$\frac{1}{3}$m,把芦苇的顶端引到岸边,苇顶和岸边水面刚好齐平,求水深和芦苇的高度. 求图中字母所代表的正方形的面积.
求图中字母所代表的正方形的面积. 如图,点A、B分别在x轴、y轴上(OA>OB),以AB为直径的圆经过原点O,C是$\widehat{AOB}$的中点,连结AC,BC.下列结论:
如图,点A、B分别在x轴、y轴上(OA>OB),以AB为直径的圆经过原点O,C是$\widehat{AOB}$的中点,连结AC,BC.下列结论: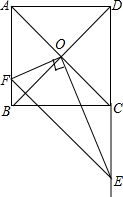 如图,边长为8的正方形的对角线AC与BD相交于O,点E是边DC延长线上的一点,点F是边AB上的一点,且OE⊥OF,EF=10,则△OEF的面积为20.
如图,边长为8的正方形的对角线AC与BD相交于O,点E是边DC延长线上的一点,点F是边AB上的一点,且OE⊥OF,EF=10,则△OEF的面积为20.