题目内容
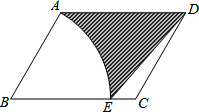
16．
如图，已知DE∥BC，AB=AC，∠1=125°，则∠C的度数是（ ）| A． | 55° | B． | 45° | C． | 35° | D． | 65° |
分析 首先根据∠1=125°，求出∠ADE的度数；然后根据DE∥BC，AB=AC，可得AD=AE，∠C=∠AED，求出∠AED的度数，即可判断出∠C的度数是多少．
解答 解：∵∠1=125°，
∴∠ADE=180°-125°=55°，
∵DE∥BC，AB=AC，
∴AD=AE，∠C=∠AED，
∴∠AED=∠ADE=55°，
又∵∠C=∠AED，
∴∠C=55°．
故选：A．
点评 （1）此题主要考查了等腰三角形的性质和应用，考查了分类讨论思想的应用，要熟练掌握，解答此题的关键是要明确：①等腰三角形的两腰相等．②等腰三角形的两个底角相等．③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．
（2）此题还考查了平行线的性质，要熟练掌握，解答此题的关键是要明确：两条平行线之间的距离处处相等．
练习册系列答案
相关题目
如图，某人将一块正五边形玻璃打碎成四块，现要到玻璃店配一块完全一样的玻璃，那么最省事的方法是带①块．
4．
如图，在平行四边形ABCD中，AB=4，AD=5，∠B=60°，以点B为圆心，BA为半径作圆，交BC边于点E，连接ED，则图中阴影部分的面积为9$\sqrt{3}$-$\frac{8}{3}π$．
如图，在平行四边形ABCD中，AB=4，AD=5，∠B=60°，以点B为圆心，BA为半径作圆，交BC边于点E，连接ED，则图中阴影部分的面积为9$\sqrt{3}$-$\frac{8}{3}π$．
11．不等式-4x≤5的解集是（ ）
| A． | $x≤-\frac{4}{5}$ | B． | $x≥-\frac{4}{5}$ | C． | $x≤-\frac{5}{4}$ | D． | $x≥-\frac{5}{4}$ |
甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发驶向乙地．如图，线段OA和折线BCD分别表示货车和轿车离甲地距离y（千米）与车行驶时间x（小时）之间的函数关系．请根据图象解答下列问题：
已知：如图，C是AE的中点，BC=DE，BC∥DE．
如图，已知B、C、E三点在同一条直线上，△ABC与△DCE都是等边三角形，其中线段BD交AC于点G，线段AE交CD于点F，求证：