题目内容
2.(1)先化简,后求值:$({\frac{a}{a-2}-\frac{4}{{{a^2}-2a}}})÷\frac{a+2}{a^2}$,其中a=3;(2)化简:$\frac{a}{{a}^{2}-4}$•$\frac{a+2}{{a}^{2}-3a}$-$\frac{1}{2-a}$,并求值,其中a与2和3构成△ABC的三边,且a为整数.
分析 (1)先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再根据三角形的三边关系求出a的值,代入原式进行计算即可.
解答 解:(1)原式=[$\frac{a}{a-2}$-$\frac{4}{a(a-2)}$]•$\frac{{a}^{2}}{a+2}$
=$\frac{(a+2)(a-2)}{a(a-2)}$•$\frac{{a}^{2}}{a+2}$
=$\frac{a+2}{a}$•$\frac{{a}^{2}}{a+2}$
=a.
当a=3时,原式=3;
(2)原式=$\frac{a}{(a+2)(a-2)}$•$\frac{a+2}{a(a-3)}$+$\frac{1}{a-2}$
=$\frac{1}{(a-2)(a-3)}$+$\frac{a-3}{(a-2)(a-3)}$
=$\frac{a-2}{(a-2)(a-3)}$
=$\frac{1}{a-3}$,
∵a与2和3构成△ABC的三边,且a为整数,
∴1<a<5,
∴当a=4时,原式=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
17.分式$-\frac{1}{{6{x^2}y}}$和$\frac{1}{2xyz}$最简公分母是( )
| A. | -6xyz | B. | 6x2yz | C. | 12xyz | D. | 12x2yz |
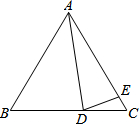 在△ABC中,AB=AC,∠BAD=40°,AE=AD,求∠EDC的度数.
在△ABC中,AB=AC,∠BAD=40°,AE=AD,求∠EDC的度数. 如图所示,△ABC沿射线XY的方向平移一定距离后成为△DEF,找出图中存在的平行且相等的三条线段是AD∥CF,AD=CF=BE.
如图所示,△ABC沿射线XY的方向平移一定距离后成为△DEF,找出图中存在的平行且相等的三条线段是AD∥CF,AD=CF=BE.