题目内容
8. 如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.(1)判断FC与AD的数量关系,并说明理由;
(2)若AB=BC+AD,则BE⊥AF吗?为什么?
(3)在(2)的条件下,若EC⊥BF,EC=3,求点E到AB的距离.
分析 (1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答;
(2)由(1)知△ADE≌△FCE,得到AE=EF,AD=CF,由于AB=BC+AD,等量代换得到AB=BC+CF,即AB=BF,证得△ABE≌△FBE,即可得到结论;
(3)在(2)的条件下有△ABE≌△FBE,得到∠ABE=∠FBE,根据角平分线的性质即可得到结果.
解答 证明:(1)∵AD∥BC,
∴∠ADC=∠ECF,
∵E是CD的中点,
∴DE=EC,
∵在△ADE与△FCE中,$\left\{\begin{array}{l}{∠ADC=∠ECF}\\{DE=EC}\\{∠AED=∠CEF}\end{array}\right.$,
∴△ADE≌△FCE(ASA),
∴FC=AD;
(2)由(1)知△ADE≌△FCE,
∴AE=EF,AD=CF,
∵AB=BC+AD,
∴AB=BC+CF,
即AB=BF,在△ABE与△FBE中,$\left\{\begin{array}{l}{AB=BF}\\{AE=EF}\\{BE=BE}\end{array}\right.$,
∴△ABE≌△FBE,
∴∠AEB=∠FBE=90°,
∴BE⊥AE;
(3)在(2)的条件下有△ABE≌△FBE,
∴∠ABE=∠FBE,∴E到BF的距离等于E到AB的距离,
∵CE⊥BF,CE=3,
∴点E到AB的距离为3.
点评 本题考查了全等三角形的判定和性质,角平分线的性质,平行线的性质,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | 同位角相等 | B. | 对顶角相等 | ||
| C. | 相等的角一定是对顶角 | D. | 角的大小与边的长短有关 |
3.为了解某校1800名学生的身高情况,从中抽取了200名学生的身高,就这个问题来说,下面结论正确的是( )
| A. | 1800名学生是总体 | B. | 1800名学生的身高是总体 | ||
| C. | 200名学生是所抽取的一个样本 | D. | 每个学生是个体 |
13.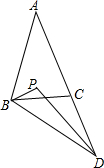 如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是∠ABD和∠ADB的平分线的交点,则∠BPD的度数是( )
如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是∠ABD和∠ADB的平分线的交点,则∠BPD的度数是( )
 如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是∠ABD和∠ADB的平分线的交点,则∠BPD的度数是( )
如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是∠ABD和∠ADB的平分线的交点,则∠BPD的度数是( )| A. | 105° | B. | 110° | C. | 130° | D. | 145° |
17.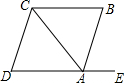 如图,点E在DA的延长线上,下列条件中能判定AB∥CD的是( )
如图,点E在DA的延长线上,下列条件中能判定AB∥CD的是( )
 如图,点E在DA的延长线上,下列条件中能判定AB∥CD的是( )
如图,点E在DA的延长线上,下列条件中能判定AB∥CD的是( )| A. | ∠B=∠BAE | B. | ∠BCA=∠CAD | C. | ∠BCA+∠CAE=180° | D. | ∠D=∠BAE |
 如图,已知AB∥CD,∠A=60°,∠C=20°,则∠E=40°.
如图,已知AB∥CD,∠A=60°,∠C=20°,则∠E=40°. 如图,一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.
如图,一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.