题目内容
 如图,某海关缉私艇在C处发现在北偏东30°方向40km的A处有一艘可疑船只,测得它正以60km/h的速度向正东方向航行,缉私艇随即以60
如图,某海关缉私艇在C处发现在北偏东30°方向40km的A处有一艘可疑船只,测得它正以60km/h的速度向正东方向航行,缉私艇随即以60| 3 |
(1)缉私艇从C处到B处需航行多长时间?
(2)缉私艇的航行方向是北偏东多少度?
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)过A作AD⊥CD于点D,可得∠DCA=30°,在Rt△ACD中,分别求出AD和CD的长度,然后设缉私艇从C处到B处需航行的时间为t,根据勾股定理可得CD2+BD2=BC2,求出时间t即可;
(2)求出BC的长度,然后根据CD的长度,求出cos∠BCD的值,继而可求得∠BCD的度数.
(2)求出BC的长度,然后根据CD的长度,求出cos∠BCD的值,继而可求得∠BCD的度数.
解答:解:过A作AD⊥CD于点D,则∠DCA=30°,
 ∵AC=40km,
∵AC=40km,
∴AD=20km,CD=20
km,
设缉私艇从C处到B处需航行的时间为t,
在Rt△BCD中.
∵CD2+BD2=BC2,
∴1200+(60t+20)2=(60
t)2,
解得:t=-
(不合题意,舍去)或t=
,
答:缉私艇从C处到B处需航行
小时;
(2)BC=
×60
=40
,
则cos∠BCD=
=
=
,
则∠BCD=60°,
即缉私艇的航行方向是北偏东60°.
 ∵AC=40km,
∵AC=40km,∴AD=20km,CD=20
| 3 |
设缉私艇从C处到B处需航行的时间为t,
在Rt△BCD中.
∵CD2+BD2=BC2,
∴1200+(60t+20)2=(60
| 3 |
解得:t=-
| 1 |
| 3 |
| 2 |
| 3 |
答:缉私艇从C处到B处需航行
| 2 |
| 3 |
(2)BC=
| 2 |
| 3 |
| 3 |
| 3 |
则cos∠BCD=
| CD |
| BC |
20
| ||
40
|
| 1 |
| 2 |
则∠BCD=60°,
即缉私艇的航行方向是北偏东60°.
点评:本题考查了解直角三角形的应用,解答本题的关键是根据方向角构造直角三角形,结合图形利用勾股定理和三角函数的知识解决问题.

练习册系列答案
相关题目
| 4 |
| A、2 | B、-2 | C、4 | D、±2 |
 如图,在四边形ABCD中,AC=BD=6,E,F,G,H分别是AB,BC,CD,DA的中点,求EG2+FH2的值.
如图,在四边形ABCD中,AC=BD=6,E,F,G,H分别是AB,BC,CD,DA的中点,求EG2+FH2的值. 和频数分布直方图.
和频数分布直方图.



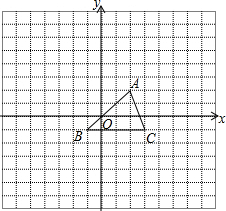 如图,方格纸中的每个小方格都是边长为1的正方形,我们把顶点在网格交点上的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点A的坐标为(2,2).
如图,方格纸中的每个小方格都是边长为1的正方形,我们把顶点在网格交点上的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点A的坐标为(2,2).