题目内容
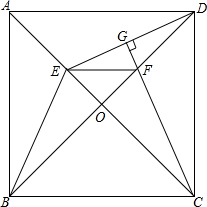 如图,正方形ABCD的对角线AC、BD相交于点O,点E是OA上任意的一点,连接BE、DE.CG⊥DE于点G,交OD于点F,连接EF.求证:四边形EBCF是等腰梯形.
如图,正方形ABCD的对角线AC、BD相交于点O,点E是OA上任意的一点,连接BE、DE.CG⊥DE于点G,交OD于点F,连接EF.求证:四边形EBCF是等腰梯形.考点:等腰梯形的判定
专题:证明题
分析:先根据正方形ABCD的对角线AC、BD相交于点O得出AC=BD,AC⊥BD,OA=OB=OC=OD,AC是∠BCD的平分线,故可得出BE=DE,∠EBO=∠EDO,再根据CG⊥DE于点G可知∠OCF+∠CEG=90°,再由∠CEG+∠EDO=90°可知∠EDO=∠OCF,故∠EBO=∠EDO,再由ASA定理可得出△OBE≌△OCF,故OE=OF,由此可得出BE=CF,再由BF=CE可知EF∥BC,由此可得出结论.
解答:证明:∵正方形ABCD的对角线AC、BD相交于点O,
∴AC=BD,AC⊥BD,OA=OB=OC=OD,AC是∠BCD的平分线,
∴BE=DE,∠EBO=∠EDO.
∵CG⊥DE于点G,
∴∠OCF+∠CEG=90°,
∵∠CEG+∠EDO=90°,
∴∠EDO=∠OCF,
∴∠EBO=∠EDO,
在△OBE与△OCF中,
∵
,
∴△OBE≌△OCF(ASA),
∴OE=OF,BE=CF.
∵OB=OC,
∴BE=CF,
∵OB=OC,
∴BF=CE,
∴EF∥BC,
∴四边形EBCF是等腰梯形.
∴AC=BD,AC⊥BD,OA=OB=OC=OD,AC是∠BCD的平分线,
∴BE=DE,∠EBO=∠EDO.
∵CG⊥DE于点G,
∴∠OCF+∠CEG=90°,
∵∠CEG+∠EDO=90°,
∴∠EDO=∠OCF,
∴∠EBO=∠EDO,
在△OBE与△OCF中,
∵
|
∴△OBE≌△OCF(ASA),
∴OE=OF,BE=CF.
∵OB=OC,
∴BE=CF,
∵OB=OC,
∴BF=CE,
∴EF∥BC,
∴四边形EBCF是等腰梯形.
点评:本题主要考查了全等三角形的性质和等腰梯形的判定,解决本题的关键就是证明△OBE≌△OCF
进而得出结论.
进而得出结论.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
据中新社北京2012年12月8日电,2012年中国粮食总产量达到586400000吨,用科学记数法表示为( )
| A、5.864×107吨 |
| B、5.864×108吨 |
| C、5.864×109吨 |
| D、5.864×1010吨 |
在直角坐标系中,已知A(-2,1),B(0,-1),C(-1,0),D(-4,-2),E(1,-2)五个点,抛物线m:y=ax2+2ax+h+a(a,h为常数,且a<0)经过其中三个点,求a和h的值.
下列各组中,是同类项的是( )
| A、2a和3b |
| B、mn和-2mn |
| C、2xy和xy2 |
| D、xy和xy2 |
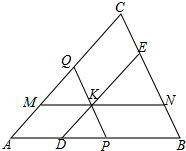 如图,K是△ABC内的任一点,过点K的直线DE∥AC于D,交BC于E;又MN∥AB,交AC于M,交BC于N;又PQ∥BC,交AB于P,交AC于Q.求证:
如图,K是△ABC内的任一点,过点K的直线DE∥AC于D,交BC于E;又MN∥AB,交AC于M,交BC于N;又PQ∥BC,交AB于P,交AC于Q.求证: