题目内容
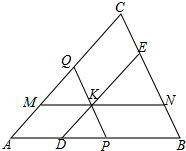如图，K是△ABC内的任一点，过点K的直线DE∥AC于D，交BC于E；又MN∥AB，交AC于M，交BC于N；又PQ∥BC，交AB于P，交AC于Q．求证：| MN |
| AB |
| DE |
| AC |
| PQ |
| BC |
考点：平行线分线段成比例
专题：证明题
分析：根据平行线分线段成比例，可得DE：=BD：AB，PQ：BC=AP：AB，根据等量代换，线段的和差，可得答案．
解答：证明：过点K的直线DE∥AC于D，交BC于E；又MN∥AB，交AC于M，交BC于N；又PQ∥BC，交AB于P，交AC于Q，
+
+
=
+
+
=
=
=
=
=2
| MN |
| AB |
| DE |
| AC |
| PQ |
| BC |
| KM+KN |
| AB |
| BD |
| AB |
| AP |
| AB |
=
| KM+BP+BD+AP |
| AB |
=
| AD+BP+BD+AP |
| AB |
=
| AD+DP+BP+BD+AD |
| AB |
=
| AB+AB |
| AB |
点评：本题考查了平行线分线段成比例，利用了平行线分线段成比例，等量代换，线段的和差．
练习册系列答案
应用题作业本系列答案
相关题目
把分式方程
-
=1去分母后所得结果正确的是（ ）
| 1 |
| x-2 |
| 1-x |
| 2-x |
| A、1-（1-x）=1 |
| B、1+（1-x）=1 |
| C、1-（1-x）=x-2 |
| D、1+（1-x）=x-2 |
如图，已知一次函数与反比例函数交于点A（-4，-2）和B（a，4），求反比例函数解析式和点B的坐标．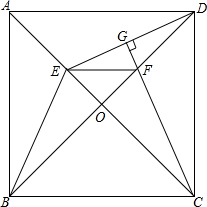
如图，正方形ABCD的对角线AC、BD相交于点O，点E是OA上任意的一点，连接BE、DE．CG⊥DE于点G，交OD于点F，连接EF．求证：四边形EBCF是等腰梯形．
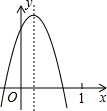已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：