题目内容
18.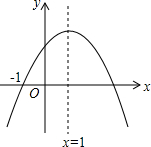 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )| A. | ac>0 | B. | 当x>1时,y随x的增大而增大 | ||
| C. | 2a+b=1 | D. | 方程ax2+bx+c=0有一个根是x=3 |
分析 根据图象可得出a<0,c>0,得出ac<0,对称轴x=1,在对称轴的右侧,y随x的增大而减小;根据x=-$\frac{b}{2a}$=1,得出b=-2a,从而得出2a+b=0;根据抛物线的对称性另一个交点到x=1的距离与-1到x=1的距离相等,得出另一个根.
解答 解:∵抛物线开口向下,∴a<0,
∵抛物线与y轴的正半轴相交,∴c>0,
∴ac<0,故A选项错误;
∵对称轴x=1,∴当x>1时,y随x的增大而减小;故B选项错误;
∵x=-$\frac{b}{2a}$=1,∴b=-2a,
∴2a+b=0,故C选项错误;
∵对称轴x=1,一个交点是(-1,0),
∴另一个交点是(3,0)
∴方程ax2+bx+c=0另一个根是x=3,故D选项正确.
故选D.
点评 本题考查了抛物线与x轴的交点问题以及二次函数的图象与系数的关系,是基础知识要熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.一种面粉的质量标识为“20±0.3㎏”,则下列面粉中合格的是( )
| A. | 19.1㎏ | B. | 19.9㎏ | C. | 20.5㎏ | D. | 20.7㎏ |
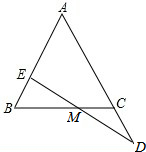 如图,在△ABC中,AB=AC,点E在AB上,点D在AC的延长线上,且BE=CD,ED交BC于点M,求证:EM=DM.
如图,在△ABC中,AB=AC,点E在AB上,点D在AC的延长线上,且BE=CD,ED交BC于点M,求证:EM=DM.