题目内容
13.已知x,y,z是实数,且满足(x-2)2+$\sqrt{y+1}$+|z-3|=0,求(x+3y)z的值.分析 根据非负数的性质列式求出x、y、z的值,然后代入代数式进行计算即可得解.
解答 解:∵(x-2)2+$\sqrt{y+1}$+|z-3|=0,
∴(x-2)2=0,且$\sqrt{y+1}$=0,且|z-3|=0.
∴x=2,且y=-1,且z=3.
∴(x+3y)z=(2-3)3=-1.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
8.若a<b,则下列各式中不成立的是( )
| A. | -3a<-3b | B. | a+2<b+2 | C. | 2-a>2-b | D. | 3a<3b |
2.计算2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷$\sqrt{3}$的结果是( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{4}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
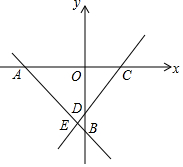 如图,直线AB交x轴,y轴于A(-3,0),B两点,直线CD交x轴,y轴于C,D(0,-2)两点,直线AB,CD相交于点E(-$\frac{1}{2}$,$-\frac{5}{2}$)
如图,直线AB交x轴,y轴于A(-3,0),B两点,直线CD交x轴,y轴于C,D(0,-2)两点,直线AB,CD相交于点E(-$\frac{1}{2}$,$-\frac{5}{2}$)