题目内容
3.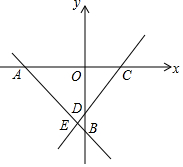 如图,直线AB交x轴,y轴于A(-3,0),B两点,直线CD交x轴,y轴于C,D(0,-2)两点,直线AB,CD相交于点E(-$\frac{1}{2}$,$-\frac{5}{2}$)
如图,直线AB交x轴,y轴于A(-3,0),B两点,直线CD交x轴,y轴于C,D(0,-2)两点,直线AB,CD相交于点E(-$\frac{1}{2}$,$-\frac{5}{2}$)(1)求两条直线的表达式;
(2)求△ACE的面积.
分析 (1)设直线AB的解析式为y1=k1x+b1,设直线CD的解析式为y2=k2x-2,由题意列方程或方程组即可得到结论;
(2)作EF⊥x轴根据三角形的面积公式即可得到结论.
解答  解:(1)设直线AB的解析式为y1=k1x+b1,由题意得$\left\{\begin{array}{l}{-3{k}_{1}+{b}_{1}=0}\\{-\frac{1}{2}{k}_{1}+{b}_{1}=-\frac{5}{2}}\end{array}\right.$,
解:(1)设直线AB的解析式为y1=k1x+b1,由题意得$\left\{\begin{array}{l}{-3{k}_{1}+{b}_{1}=0}\\{-\frac{1}{2}{k}_{1}+{b}_{1}=-\frac{5}{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-1}\\{{b}_{1}=-3}\end{array}\right.$,
∴直线AB的解析式为y1=-x-3,
设直线CD的解析式为y2=k2x-2,由题意得-$\frac{1}{2}$k2-2=-$\frac{5}{2}$,
解得:k2=1,
∴直线CD的解析式为y2=x-2;
(2)作EF⊥x轴,
∴EF=$\frac{5}{2}$,
于是得到C(2,0),
∴AC=5,
∴△ACE的面积=$\frac{1}{2}$×5×$\frac{5}{2}$=$\frac{25}{4}$.
点评 本题考查了两直线相交与平行问题,求函数的解析式,三角形面积的计算,正确的识别图形是解题的关键.

练习册系列答案
相关题目
13.下列调查中,最适宜采用普查方式的是( )
| A. | 对我国初中学生视力状况的调查 | |
| B. | 对“最强大脑”节目收视率的调查 | |
| C. | 对一批节能灯管使用寿命的调查 | |
| D. | 对量子科学通信卫星上某种零部件的调查 |
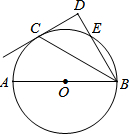 如图,点C在以AB为直径的⊙O上,BD与过点C的切线垂直于点D,BD与⊙O交于点E.
如图,点C在以AB为直径的⊙O上,BD与过点C的切线垂直于点D,BD与⊙O交于点E. 如图,AB是一条公路,点C处是水厂,点D处是村庄,该村庄的村委会有如下规划:
如图,AB是一条公路,点C处是水厂,点D处是村庄,该村庄的村委会有如下规划: