题目内容
3. 如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F,证明:DF∥BE.
如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F,证明:DF∥BE.
分析 由四边形的内角和为360度求出∠ADC+∠ABC度数,由DF、BE分别为角平分线,利用角平分线定义及等量代换得到∠ABE+∠FDC为90度,再由直角三角形ADF两锐角互余及∠ADF=∠FDC,利用等量代换得到一对同位角相等,利用同位角相等两直线平行即可得证.
解答 证明:∵四边形ABCD中,∠A=∠C=90°,
∴∠ADC+∠ABC=180°,
∵BE平分∠ABC交CD于E,DF平分∠ADC交AB于F,
∴∠ADF=∠FDC,∠ABE=∠CBE,
∴∠ABE+∠FDC=90°,
∵∠AFD+∠ADF=90°,∠ADF=∠FDC,
∴∠AFD=∠ABE,
∴BE∥DF.
点评 此题考查了平行线的判定,以及多边形的内角和,熟练掌握平行线的判定是解本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
12.二次根式a+$\sqrt{b}$的有理化因式是( )
| A. | (a+$\sqrt{b}$)2 | B. | (a-$\sqrt{b}$)2 | C. | a-$\sqrt{b}$ | D. | a+$\sqrt{b}$ |
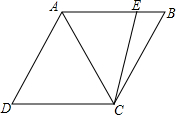 如图,在菱形ABCD中,AC=AB=4cm,点E是AB边上的动点,当BE=1cm时,作出线段CE绕点C逆时针旋转60°后,得到的线段CF,并求DF的长度.连接EF,当点E运动到什么位置时,△CEF周长有最小值?求出这个最小值.
如图,在菱形ABCD中,AC=AB=4cm,点E是AB边上的动点,当BE=1cm时,作出线段CE绕点C逆时针旋转60°后,得到的线段CF,并求DF的长度.连接EF,当点E运动到什么位置时,△CEF周长有最小值?求出这个最小值.
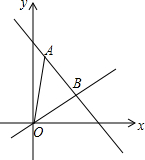 如图,在平面直角坐标系中,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与正比例函数$y=\frac{2}{3}x$的图象的交点.
如图,在平面直角坐标系中,一次函数y=kx+5的图象经过点A(1,4),点B是一次函数y=kx+5的图象与正比例函数$y=\frac{2}{3}x$的图象的交点.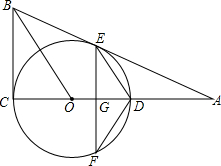 如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连结BO、ED,有BO∥ED,作弦EF⊥AC于G,连结DF.
如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连结BO、ED,有BO∥ED,作弦EF⊥AC于G,连结DF.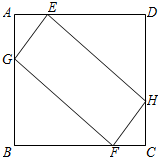 如图,边长为4的正方形ABCD中,AE=CF=1,点G、H分别是边AB、CD上的动点,且AG=CH.
如图,边长为4的正方形ABCD中,AE=CF=1,点G、H分别是边AB、CD上的动点,且AG=CH.