题目内容
15.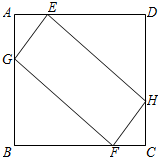 如图,边长为4的正方形ABCD中,AE=CF=1,点G、H分别是边AB、CD上的动点,且AG=CH.
如图,边长为4的正方形ABCD中,AE=CF=1,点G、H分别是边AB、CD上的动点,且AG=CH.(1)判断四边形EGFH的形状,并说明理由;
(2)当AG的长为1或3时,四边形EGFH为矩形;
(3)设四边形EGFH的周长为L,则L的范围是$2\sqrt{5}+2\sqrt{13}≤L≤8\sqrt{2}$.
分析 (1)根据全等三角形的判定和性质得出EG=FH,EH=GF,即可证明是平行四边形.
(2)根据相似三角形得出AG的长即可.
(3)根据勾股定理解答即可.
解答 解:(1)四边形EGFH是平行四边形;
理由如下:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA=4,
在Rt△AEG和△CFH中,
$\left\{\begin{array}{l}{AE=CF}&{\;}\\{∠A=∠C}&{\;}\\{AG=CH}&{\;}\end{array}\right.$,
∴Rt△AEG≌△CFH(SAS),
∴EG=FH,
同理:EH=GF,
∴四边形EGFH是平行四边形;
(2)当AG的长为1或3时,四边形EGFH为矩形;
理由:设AG=x,则BG=4-x,BF=3,
当四边形EGFH为矩形时,∠EGF=90°,
∴∠AGE+∠BGF=90°,
∵∠AGE+∠AEG=90°,
∴AEG=∠BGF,
又∵∠A=∠B=90°,
∴△AEG∽△BGF,
∴$\frac{AG}{BF}=\frac{AE}{BG}$,
即$\frac{x}{3}=\frac{1}{4-x}$,
解得:x=1,或x=3,
故答案为:1或3.
(3)当点G和点H运动到AB和CD的中点时,四边形EGFH的周长最小,
EG=$\sqrt{{1}^{2}+{2}^{2}}=\sqrt{5}$,GF=$\sqrt{{2}^{2}+{3}^{2}}=\sqrt{13}$,
所以四边形EGFH的周长为:$2\sqrt{5}+2\sqrt{13}$,
当点G和点H运动到AE=AG,CF=CH时,四边形EGFH的周长最大,
EG=$\sqrt{{1}^{2}+{1}^{2}}=\sqrt{2}$,GF=$\sqrt{{3}^{2}+{3}^{2}}=3\sqrt{2}$,
所以四边形EGFH的周长为:8$\sqrt{2}$,
所以L的范围是$2\sqrt{5}+2\sqrt{13}≤L≤8\sqrt{2}$.
点评 此题考查正方形的性质,关键是根据全等三角形的判定和性质证明四边形EGFH是平行四边形.

 科学实验活动册系列答案
科学实验活动册系列答案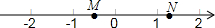 如图,M,N两点在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,M,N两点在数轴上表示的数分别是m,n,则下列式子中成立的是( )| A. | m-1<n-1 | B. | -m<-n | C. | |m|-|n|>0 | D. | m+n<0 |
 如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F,证明:DF∥BE.
如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F,证明:DF∥BE.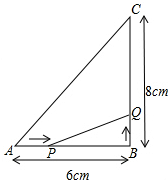 如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.