题目内容
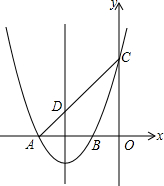 如图,已知抛物线y=x2+6x+5交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(-1,0).
如图,已知抛物线y=x2+6x+5交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(-1,0).(1)求抛物线的对称轴及点A的坐标;
(2)在平面直角坐标系xOy中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由;
(3)连结CA与抛物线的对称轴交于点D,在抛物线上是否存在点M,使得直线EM把四边形DEOC分成面积相等的两部分?若存在,请求出直线EM的解析式;若不存在,请说明理由.
考点:二次函数综合题,待定系数法求一次函数解析式,平行四边形的性质,平移的性质
专题:综合题
分析:(1)只需根据对称轴方程x=-
就可求出该抛物线的对称轴,只需令y=0就可求出点A的坐标;
(2)可分AB为平行四边形的一边和对角线两种情况讨论,然后利用平行四边形的性质和平移的性质就可解决问题;
(3)设直线EM与y轴交于点F,可先求出点D的坐标,然后求出四边形DEOC的面积,即可得到△EOF的面积,就可求出点F的坐标,然后运用待定系数法就可求出直线EM的解析式.
| b |
| 2a |
(2)可分AB为平行四边形的一边和对角线两种情况讨论,然后利用平行四边形的性质和平移的性质就可解决问题;
(3)设直线EM与y轴交于点F,可先求出点D的坐标,然后求出四边形DEOC的面积,即可得到△EOF的面积,就可求出点F的坐标,然后运用待定系数法就可求出直线EM的解析式.
解答:解:(1)抛物线的对称轴为x=-
=-3;
当y=0时,有x2+6x+5=0,
解得:x1=-1,x2=-5,
∴点A的坐标为(-5,0).
(2)当x=0时,y=5,则点C的坐标为(0,5).
①若AB为平行四边形的一边,如图1,
则有PC∥AB,PC=AB=-1-(-5)=4,
∴点P的坐标为(0+4,5)或(0-4,5),
即点P的坐标为(4,5)或(-4,5);
②若AB为平行四边形的一条对角线,如图1,
则有BP∥CA,BP=CA.
∵点C(0,5)向左平移5个单位再向下平移5个单位到点A(-5,0),
∴点B(-1,0)向左平移5个单位再向下平移5个单位到点P,
∴点P的坐标为(-1-5,0-5)即(-6,-5).
综上所述:满足条件的点P有三个,分别为(4,5),(-4,5),(-6,-5).
(3)在抛物线上存在点M,使得直线EM把四边形DEOC分成面积相等的两部分.
设直线EM与y轴交于点F,则有S△EOF=
S梯形EOCD.
∵点A(-5,0),点E(-3,0),点C(0,5),
∴OA=OC=5,OE=3,AE=OA-OE=5-3=2.
∵∠AOC=90°,∴∠OAC=∠OCA=45°.
∵DE⊥x轴,∴∠EDA=∠EAD=45°,
∴ED=EA=2,
∴S梯形EOCD=
(ED+OC)•OE=
×(2+5)×3=
,
∴S△EOF=
×
=
,
∴
OE•OF=
×3×OF=
,
∴OF=
,
∴点F为(0,
).
设直线EM的解析式为y=kx+b,
∵直线EM经过点E(-3,0)和点F(0,
),
∴
,
解得:
,
∴直线EM的解析式为y=
x+
.
| 6 |
| 2×1 |
当y=0时,有x2+6x+5=0,
解得:x1=-1,x2=-5,
∴点A的坐标为(-5,0).
(2)当x=0时,y=5,则点C的坐标为(0,5).

①若AB为平行四边形的一边,如图1,
则有PC∥AB,PC=AB=-1-(-5)=4,
∴点P的坐标为(0+4,5)或(0-4,5),
即点P的坐标为(4,5)或(-4,5);
②若AB为平行四边形的一条对角线,如图1,
则有BP∥CA,BP=CA.
∵点C(0,5)向左平移5个单位再向下平移5个单位到点A(-5,0),
∴点B(-1,0)向左平移5个单位再向下平移5个单位到点P,
∴点P的坐标为(-1-5,0-5)即(-6,-5).
综上所述:满足条件的点P有三个,分别为(4,5),(-4,5),(-6,-5).
(3)在抛物线上存在点M,使得直线EM把四边形DEOC分成面积相等的两部分.
设直线EM与y轴交于点F,则有S△EOF=
| 1 |
| 2 |
∵点A(-5,0),点E(-3,0),点C(0,5),
∴OA=OC=5,OE=3,AE=OA-OE=5-3=2.
∵∠AOC=90°,∴∠OAC=∠OCA=45°.
∵DE⊥x轴,∴∠EDA=∠EAD=45°,
∴ED=EA=2,
∴S梯形EOCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 21 |
| 2 |

∴S△EOF=
| 1 |
| 2 |
| 21 |
| 2 |
| 21 |
| 4 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 21 |
| 4 |
∴OF=
| 7 |
| 2 |
∴点F为(0,
| 7 |
| 2 |
设直线EM的解析式为y=kx+b,
∵直线EM经过点E(-3,0)和点F(0,
| 7 |
| 2 |
∴
|
解得:
|
∴直线EM的解析式为y=
| 7 |
| 6 |
| 7 |
| 2 |
点评:本题主要考查了用待定系数法求直线的解析式、抛物线的性质、平行四边形的性质、旋转的性质、等腰三角形的判定与性质等知识,运用分类讨论的思想是解决第(2)小题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
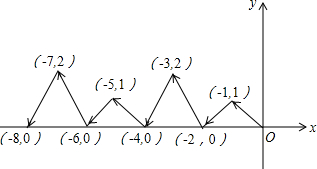 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(-1,1),第2次接着运动到点(-2,0),第3次接着运动到点(-3,2),…,按这样的运动规律,经过第2015次运动后,动点P的坐标是( )
如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(-1,1),第2次接着运动到点(-2,0),第3次接着运动到点(-3,2),…,按这样的运动规律,经过第2015次运动后,动点P的坐标是( )| A、(-2015,0) |
| B、(-2015,1) |
| C、(-2015,2) |
| D、(2015,0) |
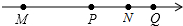 如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )| A、点M | B、点N | C、点P | D、点Q |
下列说法中,正确的是( )
| A、生活中,如果一个事件不是不可能事件,那么它就必然发生 |
| B、生活中,如果一个事件可能发生,那么它就是必然事件 |
| C、生活中,如果一个事件发生的可能性很大,那么它也可能不发生 |
| D、生活中,如果一个事件不是必然事件,那么它就不可能发生 |
下列事件属必然事件的是( )
| A、打开电视,正在直播NBA篮球赛 |
| B、早晨太阳一定从东方升起 |
| C、掷两次硬币,一定有一次正面朝上 |
| D、365人中一定有两人同一天出生 |
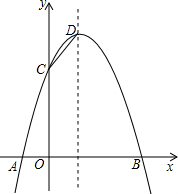 如图,已知抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).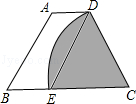 如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=6,则扇形CDE(阴影部分)的面积是( )
如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=6,则扇形CDE(阴影部分)的面积是( )