题目内容
19.问题情境:2014年某生产合作社共收获山药500吨,原计划采用批发的形式进行销售.受天气、交通等因素的影响,需要提前完成销售任务,销售时,在保持每天批发量不变的情况下,同时采用零售的方式销售,且零售量是批发量的25%,结果提前5天完成销售任务.展示交流:根据题意,甲、乙两位同学分别列出了尚不完整的方程如下:
甲:$\frac{500}{x}$-$\frac{500}{x(1+25%)}$=?
乙:$\frac{500}{x}$×(1+25%)=$\frac{500}{?}$
根据甲、乙两位同学所列的方程,请你完成下列问题:
(1)在甲所列的方程中,未知数“x”表示的意义是每天批发x吨;
(2)在乙所列的方程中,代数式“$\frac{500}{x}$×(1+25%)”表示的意义是每天零售加批发的销量;
解决问题:求该合作社每天的批发量是多少吨?(写出完整的解答过程)
拓展反思:如果每吨山药投入的成本是1000元,每吨的批发价是3000元,每吨的零售价是3500元,请你计算在实际销售中,平均每吨的利润比原计划每吨的利润增加了百分之几?
分析 (1)甲中x表示每天批发x吨;
(2)乙中$\frac{500}{x}$×(1+25%)”表示的意义是每天零售加批发的销量;
解决问题:设每天批发x吨,由题意得等量关系:全部批发所用时间-批发价零售所用时间=5,根据等量关系列出方程,再解即可;
拓展反思,根据题意可得批发所赚总利润,批发加零售所赚总利润:再计算增加百分比即可.
解答 解:(1)在甲所列的方程中,未知数“x”表示的意义是每天批发x吨;
(2)在乙所列的方程中,代数式“$\frac{500}{x}$×(1+25%)”表示的意义是每天零售加批发的销量;
解决问题:设每天批发x吨,由题意得:
$\frac{500}{x}$-$\frac{500}{(1+25%)x}$=5,
解得:x=20,
经检验:x=20是原分式方程的解,
答:该合作社每天的批发量是20吨.
拓展反思:计划总利润(3000-1000)×500=1000000元;
实际总利润:500÷[20×(1+25%)]×20×(3000-1000)+(500-20×2)×(3500-1000)=1050000元;
利润增加:(1050000-1000000)÷1000000×100%=5%,
答:平均每吨的利润比原计划每吨的利润增加了5%.
点评 此题主要考查了分式方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程,注意不要忘记检验.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
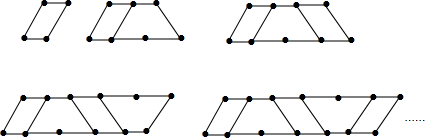
3.把一张纸剪成5块,从所得纸片中取一块,把此块再剪成5块,然后从这5块中取出一块,把此块又剪成5块,这样类似进行n次后(n是正整数),共得纸片的总块数是( )
| A. | 5n+4 | B. | 5n+5 | C. | 4n+1 | D. | 4n+4 |
 如图,直线l∥m∥n,等边△ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹的角为25°,则∠α的度数为35度.
如图,直线l∥m∥n,等边△ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹的角为25°,则∠α的度数为35度.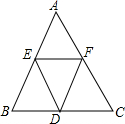 如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?
如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?