题目内容
11.先化简,再求值:$\frac{a}{a+b}$+$\frac{b}{a-b}$-$\frac{{b}^{2}}{{a}^{2}-{b}^{2}}$,将$\frac{a}{b}$=$\frac{3}{2}$代入求值.分析 原式通分并利用同分母分式的加减法则计算得到最简结果,把已知等式代入计算即可求出值.
解答 解:原式=$\frac{{a}^{2}-ab+ab+{b}^{2}}{{a}^{2}-{b}^{2}}$-$\frac{{b}^{2}}{{a}^{2}-{b}^{2}}$
=$\frac{a^2}{{{a^2}-{b^2}}}$
=$\frac{(\frac{a}{b})^{2}}{(\frac{a}{b})^{2}-1}$,
把$\frac{a}{b}$=$\frac{3}{2}$代入得:原式=$\frac{\frac{9}{4}}{\frac{9}{4}-1}$=$\frac{9}{5}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
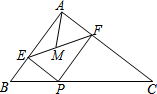 如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是$\frac{30}{13}$≤AM≤6.
如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是$\frac{30}{13}$≤AM≤6. 如图,小亮从A点出发前进5m,向右转15°,再前进5m,又向右转15°…,这样一直走下去,他第一次回到出发点A时,一共走了120m.
如图,小亮从A点出发前进5m,向右转15°,再前进5m,又向右转15°…,这样一直走下去,他第一次回到出发点A时,一共走了120m.