题目内容
2.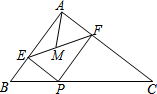 如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是$\frac{30}{13}$≤AM≤6.
如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是$\frac{30}{13}$≤AM≤6.
分析 首先连接AP,由在Rt△ABC中,∠BAC=90°,PE⊥AB于E,PF⊥AC于F,可证得四边形AEPF是矩形,即可得AP=EF,即AP=2AM,然后由当AP⊥BC时,AP最小,可求得AM的最小值,又由AP≤AC,即可求得AM的取值范围.
解答 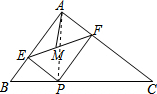 解:连接AP,
解:连接AP,
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,
∵∠BAC=90°,
∴四边形AEPF是矩形,
∴AP=EF,
∵∠BAC=90°,M为EF中点,
∴AM=$\frac{1}{2}$EF=$\frac{1}{2}$AP,
∵在Rt△ABC中,∠BAC=90°,AB=5,AC=12,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=13,
当AP⊥BC时,AP值最小,
此时S△BAC=$\frac{1}{2}$×5×12=$\frac{1}{2}$×13×AP,
∴AP=$\frac{60}{13}$,
即AP的范围是AP≥$\frac{60}{13}$,
∴2AM≥$\frac{60}{13}$,
∴AM的范围是AM≥$\frac{30}{13}$,
∵AP≤AC,
即AP≤12,
∴AM≤6,
∴$\frac{30}{13}$≤AM≤6.
故答案为:$\frac{30}{13}$≤AM≤6.
点评 此题考查了矩形的判定与性质、勾股定理以及直角三角形的面积问题.注意掌握辅助线的作法,注意当AP⊥BC时,AP最小,且AP≤AC.

练习册系列答案
相关题目
12. 如图所示的几何体,它的左视图是( )
如图所示的几何体,它的左视图是( )
 如图所示的几何体,它的左视图是( )
如图所示的几何体,它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
7.下列各式中计算正确的是( )
| A. | (x4)3=x7 | B. | (-a2)5=-a10 | C. | b5•b5=b25 | D. | a6÷a2=a3 |
12.下列关于x的方程中,一定是一元二次方程的为( )
| A. | ax2+bx+c=0 | B. | x+y=2 | C. | x2+3y-5=0 | D. | x2-1=0 |
 夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为250m,且桥宽忽略不计,则小桥总长为125 m.
夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为250m,且桥宽忽略不计,则小桥总长为125 m.