题目内容
1．若一个正多边形的每一个外角都是30°，则这个正多边形的内角和的度数等于1800°．分析 根据任何多边形的外角和都是360°，利用360除以外角的度数就可以求出外角和中外角的个数，即多边形的边数．n边形的内角和是（n-2）•180°，把多边形的边数代入公式，就得到多边形的内角和．
解答 解：多边形的边数：360°÷30°=12，
正多边形的内角和：（12-2）•180°=1800°，
故答案为：1800°．
点评 根据外角和的大小与多边形的边数无关，由外角和求正多边形的边数，是常见的题目，需要熟练掌握．
练习册系列答案
相关题目
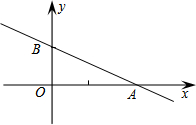如图，在以点O为原点的直角坐标系中，一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于A，与y轴交于点B，点C在第二象限内且为直线AB上一点，OC=$\frac{1}{2}$AB，反比例函数y=$\frac{k}{x}$的图象经过点C，则k的值为-$\frac{11}{50}$．
12．
如图所示的几何体，它的左视图是（ ）
如图所示的几何体，它的左视图是（ ）| A． |  | B． |  | C． |  | D． |  |
16．下列各式能用完全平方式进行分解因式的是（ ）
| A． | x2+1 | B． | x2+2x-1 | C． | x2+x+1 | D． | ${x^2}-x+\frac{1}{4}$ |
6．下列手机软件图标中，属于中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |