题目内容
18.已知关于x的方程 x2-(2k+1)x+4(k-$\frac{1}{2}$)=0.若等腰三角形ABC的一边长a=4,另两边边长b、c恰好是这个方程的两个实数根,则△ABC的周长为10.分析 分a为腰长以及底边长两种情况考虑.①等a为腰长时,将x=4代入原方程可求出k值,将k值代入原方程解方程可得出底边长,再利用三角形的三边关系验证后可得出结论;②当a为底边长时,根据根的判别式△=0即可求出k值,将k值代入原方程解方程可得出腰长,再利用三角形的三边关系验证后即可得出结论.综上即可得出结论.
解答 解:①当a为腰长时,将x=4代入x2-(2k+1)x+4(k-$\frac{1}{2}$)=0中得:10-4k=0,
解得:k=$\frac{5}{2}$,
∴原方程为x2-6x+8=0,
解得:x1=4,x2=2,
∵4,4,2满足任意两边之和大于第三边,
∴C=4+4+2=10;
②当a为底边长时,方程 x2-(2k+1)x+4(k-$\frac{1}{2}$)=0有两个相等的实数根,
∴△=[-(2k+1)]2-4×1×4(k-$\frac{1}{2}$)=4k2-12k+9=0,
解得:k=$\frac{3}{2}$.
当k=$\frac{3}{2}$时,原方程为x2-4x+4=0,
解得:x=2,
∵2,2,4不满足任意两边之和大于第三边,
∴a为底边长不符合题意.
综上可知:△ABC的周长为10.
故答案为:10.
点评 本题考查了根的判别式、三角形三边关系以及等腰三角形的性质,分a为腰长以及底边长两种情况考虑是解题的关键.

练习册系列答案
相关题目
6.下列从左到右的变形中,不是因式分解的是( )
| A. | -3x2+6xy=-3x(x-2y) | B. | a2+2ab=a(a+2b) | ||
| C. | ab-a-b+1=(a-1)(b-1) | D. | a2+2a-3=a(a+2-$\frac{3}{a}$) |
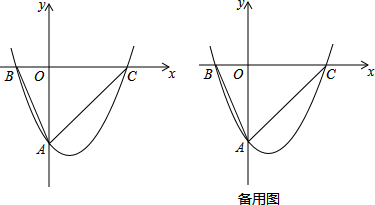
 如图,在△ABC中,AB=AC=10,sinB=$\frac{3}{5}$,
如图,在△ABC中,AB=AC=10,sinB=$\frac{3}{5}$,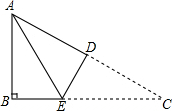 如图所示,在△ABC中,∠B=90°,将△ABC折叠,使点C与点A重合,折痕为DE,若△ABE的周长为7,AB比BC小1,则AB的长为8.
如图所示,在△ABC中,∠B=90°,将△ABC折叠,使点C与点A重合,折痕为DE,若△ABE的周长为7,AB比BC小1,则AB的长为8.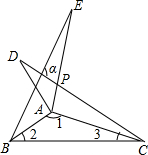 如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为108°.
如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为108°.