题目内容
11.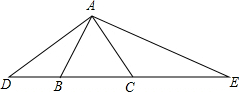 已知,如图,△ABC为等边三角形,∠DAE=120°,且∠DAE的两边交直线BC于D、E两点,
已知,如图,△ABC为等边三角形,∠DAE=120°,且∠DAE的两边交直线BC于D、E两点,(1)求证:BC2=BD•CE;
(2)若DB=1,CE=4,求BC的值.
分析 (1)先根据题意得出△ABD∽△EAC,再由相似三角形的对应边成比例即可得出结论;
(2)直接根据(1)的结论可得出答案.
解答 (1)证明:∵∠D+∠DAB=60°,∠DAB+∠EAC=60°
∴∠D=∠EAC.
又∵∠ABD=∠EAC=120°,
∴△ABD∽△EAC,
∴$\frac{AB}{AE}$=$\frac{AD}{CE}$,
∴BC2=BD•CE.
(2)解:∵DB=1,CE=4,由(1)知,BC2=BD•CE,
∴BC=2.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
2.关于x的一元二次方程mx2+$\sqrt{2m+1}$x+1=0有两个不相等的同号实数根,则m的取值范围是( )
| A. | m$<\frac{1}{2}$且m≠0 | B. | -$\frac{1}{2}≤m<\frac{1}{2}$ | C. | -$\frac{1}{2}≤m<\frac{1}{2}$且m≠0 | D. | 0$<m<\frac{1}{2}$ |
 在△ABC中,AB=AC,求作一点P,使点P为△ABC的外接圆圆心.(保留作图痕迹,不写作法)
在△ABC中,AB=AC,求作一点P,使点P为△ABC的外接圆圆心.(保留作图痕迹,不写作法)

 已知:如图,A,B,C在同一条线段上,M是线段AC的中点,N是线段BC的中点,且AM=5cm,CN=3cm.求线段AB的长.
已知:如图,A,B,C在同一条线段上,M是线段AC的中点,N是线段BC的中点,且AM=5cm,CN=3cm.求线段AB的长.