题目内容
15.阅读材料:如图1,在平面直角坐标系中,O为坐标原点,对于任意两点A (x1,y1),B(x2,y2),由勾股定理可得:AB2=(x1-x2)2+(y1-y2)2,我们把$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$叫做A、B两点之间的距离,记作AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
例题:在平面直角坐标系中,O为坐标原点,设点P(x,0).
①A(0,2),B (3,-2),则AB=5.;PA=$\sqrt{{x}^{2}+4}$.;
解:由定义有AB=$\sqrt{(0-3)^{2}+[2-(-2)]^{2}}=5$;PA=$\sqrt{(x-3)^{2}+(0-2)^{2}}=\sqrt{{x}^{2}+4}$.
②$\sqrt{(x-1)^{2}+4}$表示的几何意义是点P(x,0)到点(1,2)的距
离;$\sqrt{{x}^{2}+1}+\sqrt{(x-2)^{2}+9}$表示的几何意义是点P(x,0)分别到点(0,1)和点(2,3)的距离和.
解:因为$\sqrt{(x-1)^{2}+4}=\sqrt{(x-1)^{2}+(0-2)^{2}}$,所以$\sqrt{(x-1)^{2}+4}$表示的几何意义是点P(x,0)到点(1,2)的距
离;同理可得,$\sqrt{{x}^{2}+1}+\sqrt{(x-2)^{2}+9}$表示的几何意义是点P(x,0)分别到点(0,1)和点(2,3)的距离和.
根据以上阅读材料,解决下列问题:
(1)如图2,已知直线y=-2x+8与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(x1,y1)、B(x2,y2)两点,
则点A、B的坐标分别为A(1,6),B(3,2),AB=2$\sqrt{5}$.
(2)在(1)的条件下,设点P(x,0),则$\sqrt{(x-{x}_{1})^{2}+{y}_{1}^{2}}+\sqrt{(x-{x}_{2})^{2}+{y}_{2}^{2}}$表示的几何意义是点P(x,0)分别到点(1,6)和点(3,2)的距离和;试求$\sqrt{(x-{x}_{1})^{2}+{y}_{1}^{2}}+\sqrt{(x-{x}_{2})^{2+{y}_{2}^{2}}}$的最小值,以及取得最小值时点P的坐标.
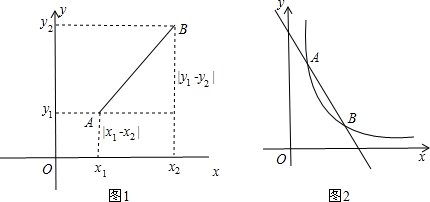
分析 (1)由直线和反比例函数解析式组成方程组,解方程组求出A、B坐标;根据两点之间的距离公式即可求出AB;
(2)根据题意容易得出表示的几何意义;作点B关于x轴的对称点B′,连接AB′交x轴于P(即为满足题意的点),则B′坐标为(3,-2),得出$\sqrt{(x-{x}_{1})^{2}+{y}_{1}^{2}}+\sqrt{(x-{x}_{2})^{2}+{y}_{2}^{2}}$的最小值=AB′,由两点之间的距离公式求出AB′即可;用待定系数法求出直线AB′的解析式,再求出直线与x轴的交点即为点P的坐标.
解答 解:(1)解方程组$\left\{\begin{array}{l}{y=-2x+8}\\{y=\frac{6}{x}}\end{array}\right.$,
得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=6}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=2}\end{array}\right.$,
∴A(1,6),B(3,2),
∴AB=$\sqrt{(1-3)^{2}+(6-2)^{2}}$=2$\sqrt{5}$;
故答案为1,6;3,2;2$\sqrt{5}$;
(2)∵$\sqrt{(x-{x}_{1})^{2}+{y}_{1}^{2}}+\sqrt{(x-{x}_{2})^{2}+{y}_{2}^{2}}$=$\sqrt{(x-1)^{2}+(0-6)^{2}}$+$\sqrt{(x-3)^{2}+(0-2)^{2}}$,
∴$\sqrt{(x-{x}_{1})^{2}+{y}_{1}^{2}}+\sqrt{(x-{x}_{2})^{2}+{y}_{2}^{2}}$表示的几何意义是点P(x,0)分别到点(1,6)和点(3,2)的距离和;
故答案为:点P(x,0)分别到点(1,6)和点(3,2)的距离和;
作点B关于x轴的对称点B′,连接AB′交x轴于P,如图所示: 则B′坐标为(3,-2),
则B′坐标为(3,-2),
∴$\sqrt{(x-{x}_{1})^{2}+{y}_{1}^{2}}+\sqrt{(x-{x}_{2})^{2}+{y}_{2}^{2}}$的最小值=AB′=$\sqrt{(1-3)^{2}+(6+2)^{2}}$=2$\sqrt{17}$;
设直线AB′的解析式为y=kx+b,
把A(1,6),B′(3,-2)代入得:$\left\{\begin{array}{l}{k+b=6}\\{3k+b=-2}\end{array}\right.$,
解得:k=-4,b=10,
∴直线 AB′的解析式为:y=-4x+10,
∵当y=0时,x=$\frac{5}{2}$,
∴点P的坐标为($\frac{5}{2}$,0).
点评 本题是反比例函数综合题目,考查了直线与双曲线的交点坐标的求法、二元一次方程组的解法、两点之间的距离公式、用待定系数法求一次函数的解析式等知识,本题难度较大,综合性强,特别是(2)中,需要通过作辅助线求出一次函数的解析式才能得出结果.

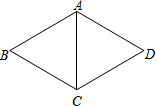 如图,在菱形ABCD中,对角线AC长为3cm,∠ABC=60°,则菱形ABCD的周长为( )
如图,在菱形ABCD中,对角线AC长为3cm,∠ABC=60°,则菱形ABCD的周长为( )| A. | 6$\sqrt{3}$cm | B. | 12$\sqrt{3}$cm | C. | 12cm | D. | 24cm |
| A. | $\frac{4}{x}$+y=5 | B. | x-y=2 | C. | $\frac{1}{2}$x2+y=0 | D. | 2x+3y=z |
 随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:
随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:| 乘车路程计价区段 | 0-10 | 11-15 | 16-20 | … |
| 对应票价(元) | 2 | 3 | 4 | … |
小明用学生卡乘车,上车时站名上对应的数字是5,下车时站名上对应的数字是22,那么,小明乘车的费用是1元.
 如图,AB∥CD,∠1=105°,∠2=140°,则∠3=65°.
如图,AB∥CD,∠1=105°,∠2=140°,则∠3=65°. 如图,是一块从一个边长为20cm的正方形BCDM材料中剪出的垫片,经测得FG=9cm,则这个剪出的图形的周长是98cm.
如图,是一块从一个边长为20cm的正方形BCDM材料中剪出的垫片,经测得FG=9cm,则这个剪出的图形的周长是98cm. 如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=114°,则∠DFC的度数为何?( )
如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=114°,则∠DFC的度数为何?( )