Question

5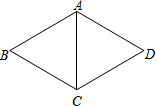．如图，在菱形ABCD中，对角线AC长为3cm，∠ABC=60°，则菱形ABCD的周长为（　　）

• A． 6$\sqrt{3}$cm
• B． 12$\sqrt{3}$cm
• C． 12cm
• D． 24cm

Answer 1

分析 由于四边形ABCD是菱形，AC是对角线，根据∠ABC=60°，而AB=BC，易证△BAC是等边三角形，从而可求AB=BC=3，即AB=BC=CD=AD=3，那么就可求菱形的周长．

解答 解：∵四边形ABCD是菱形，AC是对角线，
∴AB=BC=CD=AD，
∵∠ABC=60°，
∴△ABC是等边三角形，
∴AB=BC=3，
∴AB=BC=CD=AD=3，
∴菱形ABCD的周长是12．
故选：C．

点评 本题考查了菱形的性质、等边三角形的判定和性质．菱形的对角线平分对角，解题的关键是证明△ABC是等边三角形．