题目内容
等腰三角形底边是2,顶角是45°,面积是 .
考点:等腰直角三角形,等腰三角形的性质
专题:
分析:根据等腰直角三角形的性质,可得AD=DC=x,AC=
x,再根据勾股定理,可得DC的平方,根据三角形的面积,可得答案.
| 2 |
解答:解:如图:

作CD⊥AB与点D,
设DC=x,
∴∠ADC=90°.
∵∠A=45°,DC=x,
∴AD=DC=x,AC=
x,BD=
x-x,
在Rt△BDC中由勾股定理,得
BD2+DC2=BC2,
即(
x-x)2+x2=4,
解得x2=2+
.
S△ABC=
AB•DC=
×
x•x=
×x2=
×(2+
)=
+1,
故答案为:
+1.

作CD⊥AB与点D,
设DC=x,
∴∠ADC=90°.
∵∠A=45°,DC=x,
∴AD=DC=x,AC=
| 2 |
| 2 |
在Rt△BDC中由勾股定理,得
BD2+DC2=BC2,
即(
| 2 |
解得x2=2+
| 2 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
故答案为:
| 2 |
点评:本题考查了等腰三角形,构造直角三角形是解题关键.

练习册系列答案
相关题目
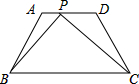 如图,在梯形ABCD中,AD∥BC,AB=CD=2,AD=5,在AD边上是否存在一点P,使得△ABP与△DPC相似?若存在,求出线段AP的长;若不存在,请说明理由.
如图,在梯形ABCD中,AD∥BC,AB=CD=2,AD=5,在AD边上是否存在一点P,使得△ABP与△DPC相似?若存在,求出线段AP的长;若不存在,请说明理由.