题目内容
 如图,BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若AD平分∠BAC,试说明:BD=CD.
如图,BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若AD平分∠BAC,试说明:BD=CD.考点:角平分线的性质,全等三角形的判定与性质
专题:证明题
分析:先根据角平分线的性质得出DE=DF,再利用ASA证明△BFD≌△CED,即可证得BD=CD.
解答:证明:∵BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,AD平分∠BAC,
∴DE=DF.
在△BFD与△CED中,
,
∴△BFD≌△CED(ASA),
∴BD=CD.
∴DE=DF.
在△BFD与△CED中,
|
∴△BFD≌△CED(ASA),
∴BD=CD.
点评:本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了全等三角形的判定与性质.

练习册系列答案
相关题目
若一组数据3,a,4,5的众数为4,则这组数据的平均数为( )
| A、3 | B、4 | C、5 | D、6 |
下列各组式子是同类项的是( )
| A、2ab2与-ba2 |
| B、-mn与mn |
| C、5x2y与-2xy2 |
| D、3a与3ab |
 如图,在梯形ABCD中,AD∥BC,∠B=90°,E是AB的中点,且DC=AD+BC,则下列结论中错误的有( )
如图,在梯形ABCD中,AD∥BC,∠B=90°,E是AB的中点,且DC=AD+BC,则下列结论中错误的有( )| A、DE平分∠ADC |
| B、△DEC是直角三角形 |
| C、点E到DC的距离为AB长的一半 |
| D、△DEC的面积为△ADE面积的2倍 |
点p(5.-3)关于原点对称的点的坐标是( )
| A、(3,-5) |
| B、(-5,-3) |
| C、(-5,3) |
| D、(-3,5) |
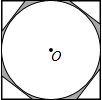 已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )
已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )A、32
| ||
B、
| ||
| C、1 | ||
| D、16-4π |
(a2)3等于( )
| A、3a2 |
| B、a5 |
| C、a6 |
| D、a8 |

 上海世博会中国馆共分为国家馆和地区馆两部分,国家馆居中升起、层叠出挑,采用极富中国建筑文化元素的红色“斗冠”造型,由地下一层、地上六层组成.小明通过上网查阅资料得知,国家馆地上六层均为正方形,如图所示,最上面一层正方形边长为a米,以下每层的边长比上一层减少b米.
上海世博会中国馆共分为国家馆和地区馆两部分,国家馆居中升起、层叠出挑,采用极富中国建筑文化元素的红色“斗冠”造型,由地下一层、地上六层组成.小明通过上网查阅资料得知,国家馆地上六层均为正方形,如图所示,最上面一层正方形边长为a米,以下每层的边长比上一层减少b米.