题目内容
5. 已知:如图,∠DAB=∠CAB,∠DBE=∠CBE,求证:AC=AD.
已知:如图,∠DAB=∠CAB,∠DBE=∠CBE,求证:AC=AD.
分析 首先根据等角的补角相等可得到∠ABC=∠ABD,再由条件∠CAE=∠DAE,AB=AB可利用ASA证明△ABC≌△ABD,再根据全等三角形对应边相等可得结论.
解答 证明:∵∠ABC+∠CBE=180°,∠ABD+∠DBE=180°,∠CBE=∠DBE,
∴∠ABC=∠ABD,
在△ABC和△ABD中,
$\left\{\begin{array}{l}{∠CAE=∠DAE}\\{AB=AB}\\{∠ABC=∠ABD}\end{array}\right.$,
∴△ABC≌△ABD(ASA),
∴AC=AD.
点评 此题主要考查了全等三角形的性质与判定,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
17.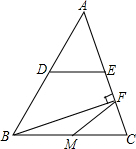 如图所示,△ABC中,BF为AC边上的高,点D、E、M分别为AB、AC、BC的中点.DE=6cm.则FM等于( )
如图所示,△ABC中,BF为AC边上的高,点D、E、M分别为AB、AC、BC的中点.DE=6cm.则FM等于( )
 如图所示,△ABC中,BF为AC边上的高,点D、E、M分别为AB、AC、BC的中点.DE=6cm.则FM等于( )
如图所示,△ABC中,BF为AC边上的高,点D、E、M分别为AB、AC、BC的中点.DE=6cm.则FM等于( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
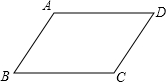 已知:如图,在四边形ABCD中,AB∥DC,AD∥BC,求证:AB=DC,AD=BC.
已知:如图,在四边形ABCD中,AB∥DC,AD∥BC,求证:AB=DC,AD=BC. 请用含字母的式子表示图形阴影部分的面积,并求阴影部分的面积.(结果保留π)
请用含字母的式子表示图形阴影部分的面积,并求阴影部分的面积.(结果保留π) 画出三角形所有的中线
画出三角形所有的中线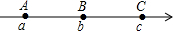 如图,数轴上的A、B、C三点所表示的数分别为a、b、c,其中AB与BC的长度相等.
如图,数轴上的A、B、C三点所表示的数分别为a、b、c,其中AB与BC的长度相等.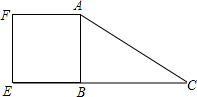 如图所示,△ABC是直角三角形,四边形ABEF是正方形,AC=15,BC=8.
如图所示,△ABC是直角三角形,四边形ABEF是正方形,AC=15,BC=8.