题目内容
15.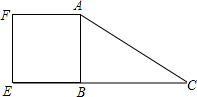 如图所示,△ABC是直角三角形,四边形ABEF是正方形,AC=15,BC=8.
如图所示,△ABC是直角三角形,四边形ABEF是正方形,AC=15,BC=8.(1)求正方形的面积;
(2)求正方形对角线的长.(精确到0.1)
分析 (1)在直角△ABC中利用勾股定理得到AB2=AC2-BC2=152-82=161,即为正方形的面积;
(2)连结AE,根据正方形的性质得出AB=BE,∠ABE=90°,利用勾股定理即可求出AE=$\sqrt{A{B}^{2}+B{E}^{2}}$,代入计算即可求解.
解答 解:(1)在直角△ABC中,∵∠ABC=90°,AC=15,BC=8,
∴AB2=AC2-BC2=152-82=161, 即正方形的面积为161;
即正方形的面积为161;
(2)连结AE.
∵四边形ABEF是正方形,
∴AB=BE,∠ABE=90°,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{161+161}$=$\sqrt{322}$≈17.9.
点评 本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.即如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.同时考查了正方形的性质.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 已知:如图,∠DAB=∠CAB,∠DBE=∠CBE,求证:AC=AD.
已知:如图,∠DAB=∠CAB,∠DBE=∠CBE,求证:AC=AD. 如图,在三角形纸片ABC中.∠A=64°,∠B=76°,将纸片的一角折叠,使点C落在△ABC内部,折痕为MN.如果∠1=17°,求∠2的度数.
如图,在三角形纸片ABC中.∠A=64°,∠B=76°,将纸片的一角折叠,使点C落在△ABC内部,折痕为MN.如果∠1=17°,求∠2的度数. 已知:如图,在△ABC中,∠BCA=2∠B,D为∠BCA的平分线上的-点,连结AD,∠D=∠B.求证:AD∥BC.
已知:如图,在△ABC中,∠BCA=2∠B,D为∠BCA的平分线上的-点,连结AD,∠D=∠B.求证:AD∥BC. 如图所示,a1、a2、a3的大小关系是a1>a2>a3.
如图所示,a1、a2、a3的大小关系是a1>a2>a3.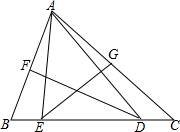 如图,在△ABC中,∠C=40°,∠B=68°,AB、AC的垂直平分线分别交BC于D、E.求∠EAD的度数.
如图,在△ABC中,∠C=40°,∠B=68°,AB、AC的垂直平分线分别交BC于D、E.求∠EAD的度数.