题目内容
13．
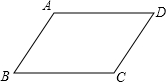已知：如图，在四边形ABCD中，AB∥DC，AD∥BC，求证：AB=DC，AD=BC．
分析 连接BD，根据平行线的性质得出∠ADB=∠CBD，∠ABD=∠CDB，根据ASA推出△ADB≌△CBD，根据全等三角形的性质得出即可
解答 证明：连接BD，
∵AB∥CD，AD∥BC，
∴∠ADB=∠CBD，∠ABD=∠CDB，
在△ADB和△CBD中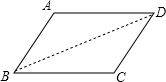
$\left\{\begin{array}{l}{∠ADB=∠CBD}\\{BD=BD}\\{∠ABD=∠CDB}\end{array}\right.$，
∴△ADB≌△CBD，
∴AD=BC，AB=CD．
点评 本题考查了全等三角形的判定和性质，平行线的性质的应用，解此题的关键是推出△ADB≌△CBD，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，全等三角形的对应边相等．
练习册系列答案
阅读快车系列答案
相关题目
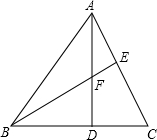如图，已知AD为△ABC的高，E为AC上的一点，BE交AD于F，且有BF=AC，FD=CD
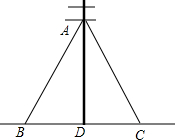如图所示，为了固定电线杆AD，将两根长分别为10m的电线一端同系在电线杆A点上，另一端固定在地面上的两个锚上，那么两个锚（B，C）离电线杆底部（D）的距离相等吗？为什么？
18．
如图，用平面去截圆柱，截面形状是（ ）
如图，用平面去截圆柱，截面形状是（ ）| A． |  | B． |  | C． |  | D． |  |
已知：如图，∠DAB=∠CAB，∠DBE=∠CBE，求证：AC=AD．
己知：在△ABC中，AD是BC边上的高，AD=BD，BE=AC，延长BE交AC于F，求证：BF是△ABC中AC边上的高．