题目内容
1. 在正方形ABCD中,O是对角线AC中点,PF丄CD于点F,PE丄PB,求证:DF=EF.
在正方形ABCD中,O是对角线AC中点,PF丄CD于点F,PE丄PB,求证:DF=EF.
分析 延长FP交AB于G,根据正方形的性质和已知推出矩形AGFD,得到DF=AG,证∠GBP=∠FPE,推出Rt△GBP≌Rt△FPE,推出EF=PG,根据等腰三角形的性质求出即可.
解答 证明:延长FP交AB于G,如图所示:
∵四边形ABCD是正方形,
∴∠BAD=∠D=90°(正方形的四个内角都是直角),
∵PF⊥CD,
∴∠DFG=90°,
∴四边形AGFD是矩形(有三个角是直角的四边形是矩形),
∴DF=AG,∠AGF=90°,
∵AC是正方形ABCD的对角线,
∴∠BAC=45°,
∴△AGP是等腰直角三角形,即AG=GP,
∴GP=DF,
同理CF=PF=BG,
∵∠GPB+∠FPE=90°,∠GPB+∠GBP=90°,
∴∠GBP=∠FPE,
在Rt△GBP和Rt△FPE中,
$\left\{\begin{array}{l}{∠GBP=∠FPE}\\{BG=PF}\\{∠BGP=∠PFE}\end{array}\right.$,
∴Rt△GBP≌Rt△FPE(ASA),
∴GP=EF,
∴DF=EF.
点评 本题主要考查等腰三角形的性质和判定、全等三角形的性质和判定、正方形的性质等知识点的连接和掌握,特别是通过作辅助线证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,一只蚂蚁以均匀的速度沿台阶A1→A2→A3→A4→A5爬行,则此蚂蚁爬行的高度h随时间t变化的图象大致是( )
如图,一只蚂蚁以均匀的速度沿台阶A1→A2→A3→A4→A5爬行,则此蚂蚁爬行的高度h随时间t变化的图象大致是( )




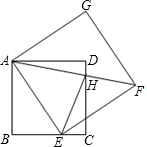 如图,E为正方形ABCD的边BC上一动点,以AE为一边作正方形AEFD,对角线AF交边CD于H,连EH.
如图,E为正方形ABCD的边BC上一动点,以AE为一边作正方形AEFD,对角线AF交边CD于H,连EH.