题目内容
15.在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥CA,DF∥BA,连接EF,则下列三种说法:①如果EF=AD,那么四边形AEDF是矩形
②如果EF⊥AD,那么四边形AEDF是菱形
③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形
其中正确的有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
分析 先根据两组对边分别平行的四边形是平行四边形可得四边形AEDF是平行四边形,再根据对角线相等的平行四边形是矩形判断①正确;根据对角线互相垂直的平行四边形是菱形判断②正确;根据等腰三角形三线合一的性质知:DA平分∠BAC,再证明平行四边形AEDF是菱形;从而判断③错误.
解答  解:∵DE∥CA,DF∥BA,
解:∵DE∥CA,DF∥BA,
∴四边形AEDF是平行四边形.
①∵EF=AD,
∴平行四边形四边形AEDF是矩形;故①正确;
②∵EF⊥AD,
∴平行四边形四边形AEDF是菱形;故②正确; ③∵AD⊥BC,AB=AC;
③∵AD⊥BC,AB=AC;
∴∠DAE=∠DAF,
∵∠DAE=∠ADF,
∴∠DAF=∠ADF,
∴DF=AF,
∴平行四边形AEDF是菱形;故③错误;
故选B.
点评 此题主要考查了矩形、菱形、正方形的判定方法:
对角线相等的平行四边形是矩形;
对角线互相垂直的平行四边形是菱形;
既是矩形、又是菱形的四边形是正方形.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
5.在平面直角坐标系中,点A(3,-5)所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.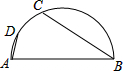 如图,AB是半圆的直径,D是弧AC的中点,∠ABC=50°,则∠DAB等于( )
如图,AB是半圆的直径,D是弧AC的中点,∠ABC=50°,则∠DAB等于( )
 如图,AB是半圆的直径,D是弧AC的中点,∠ABC=50°,则∠DAB等于( )
如图,AB是半圆的直径,D是弧AC的中点,∠ABC=50°,则∠DAB等于( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
10.已知第1组数据:1,3,5,7的方差为S12,第2组数据:52,54,56,58的方差为S22,第3组数据:2016,2015,2014,2013的方差为S32,则S12,S22,S32的大小关系是( )
| A. | S32>S22>S12 | B. | S12=S22<S32 | C. | S12=S22>S32 | D. | S12=S22=S32 |
20.3-2可以表示为( )
| A. | $\frac{1}{3×3}$ | B. | -$\frac{1}{3×3}$ | C. | 3×3 | D. | 3+3 |
7.将18个大小重量完全一样的彩球放入一个袋中,其中6个是白色的,5个是黄色的,4个是绿色的,3个是红色的,任意摸出一个彩球是红色的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{18}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{6}$ |
4.据国家统计局公布,2015年我国国内生产总值约676700亿元,676700亿元用科学记数法表示为( )
| A. | 6.767×103亿元 | B. | 6.767×104亿元 | C. | 6.767×105亿元 | D. | 6.767×106亿元 |
 如图,直线y=$\frac{1}{2}$x-2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx-2经过A,B,C,点B坐标为(-1,0).
如图,直线y=$\frac{1}{2}$x-2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx-2经过A,B,C,点B坐标为(-1,0).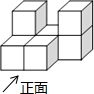 如图所示的几何体是由七个相同的小正方体组合而成的,它的左视图是( )
如图所示的几何体是由七个相同的小正方体组合而成的,它的左视图是( )


