题目内容
6. 如图,直线y=$\frac{1}{2}$x-2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx-2经过A,B,C,点B坐标为(-1,0).
如图,直线y=$\frac{1}{2}$x-2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx-2经过A,B,C,点B坐标为(-1,0).(1)求抛物线的解析式;
(2)若点D是线段AC上一个动点,DE⊥AC,交直线AC下方的抛物线于点E,EG⊥x轴于点G,交AC于点F,请求出DF长的最大值;
(3)设抛物线对称轴与x轴相交于点H,点P是射线CH上的一个动点,当△ABP是直角三角形时,请直接写出点P的坐标.
分析 (1)先利用一次函数解析式求出A和C点坐标,再设交点式y=a(x+1)(x-4),然后把C点坐标代入求出a的值即可得到抛物线解析式;
(2)设E(x,$\frac{1}{2}$x2-$\frac{3}{2}$x-2),则F(x,$\frac{1}{2}$x-2),则可表示出EF=-$\frac{1}{2}$x2+2x=-$\frac{1}{2}$(x-2)2+2,再证明Rt△DEF∽Rt△OAC,利用相似比得到DF=$\frac{\sqrt{5}}{5}$EF=-$\frac{\sqrt{5}}{10}$(x-2)2+$\frac{2\sqrt{5}}{5}$,然后利用二次函数的性质解决问题;
(3)先利用对称性确定H($\frac{3}{2}$,0),再利用待定系数法求出射线CH的解析式为y=$\frac{4}{3}$x-2(x≥0),接着分类讨论:当∠BPA=90°时,如图2,设P(t,$\frac{4}{3}$t-2),利用两点间的距离公式表示出PB2=(t+1)2+($\frac{4}{3}$t-2)2,PA2=(t-4)2+($\frac{4}{3}$t-2)2,则根据勾股定理得到(t+1)2+($\frac{4}{3}$t-2)2+(t-4)2+($\frac{4}{3}$t-2)2=52,然后解方程求出t即可得到此时P点坐标;当∠BAP′=90°时,如图2,易得P′(4,$\frac{10}{3}$).
解答 解:(1)∵当y=0时,$\frac{1}{2}$x-2=0,解得x=4,
∴A(4,0),
∵当x=0时,y=$\frac{1}{2}$x-2=-2,
∴C(0,-2),
设抛物线解析式为y=a(x+1)(x-4),
把C(0,-2)代入得a•1•(-4)=-2,解得a=$\frac{1}{2}$,
∴抛物线解析式为y=$\frac{1}{2}$(x+1)(x-4),即y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2;
(2)在Rt△AOC中,AC=$\sqrt{O{C}^{2}+O{A}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
设E(x,$\frac{1}{2}$x2-$\frac{3}{2}$x-2),则F(x,$\frac{1}{2}$x-2),
∴EF=$\frac{1}{2}$x-2-($\frac{1}{2}$x2-$\frac{3}{2}$x-2)=-$\frac{1}{2}$x2+2x=-$\frac{1}{2}$(x-2)2+2,
∵DE⊥AC,EG⊥AB,
∴∠FDE=∠AGE=90°,
而∠AFG=∠EFD,
∴∠GAF=∠DEF,
∴Rt△DEF∽Rt△OAC,
∴DF:OC=EF:AC,即DF:2=EF:2$\sqrt{5}$,
∴DF=$\frac{\sqrt{5}}{5}$EF=-$\frac{\sqrt{5}}{10}$(x-2)2+$\frac{2\sqrt{5}}{5}$,
当x=2时,DF有最大值,最大值为$\frac{2\sqrt{5}}{5}$;
(3)∵A(4,0),B(-1,0),
∴H($\frac{3}{2}$,0),
设直线CP的解析式为y=mx+n,
把C(0,-2),H($\frac{3}{2}$,0)代入得$\left\{\begin{array}{l}{n=-2}\\{\frac{3}{2}m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{4}{3}}\\{n=-2}\end{array}\right.$,
∴射线CH的解析式为y=$\frac{4}{3}$x-2(x≥0),
当∠BPA=90°时,如图2,设P(t,$\frac{4}{3}$t-2),则PB2=(t+1)2+($\frac{4}{3}$t-2)2,PA2=(t-4)2+($\frac{4}{3}$t-2)2,
∵PB2+PA2=AB2,
∴(t+1)2+($\frac{4}{3}$t-2)2+(t-4)2+($\frac{4}{3}$t-2)2=52,
整理得t2-3t=0,解得t1=0,t2=3,此时P点坐标为(0,-2)或(3,2);
当∠BAP′=90°时,如图2,则P′A⊥x轴,P′点的横坐标为4,当x=4时,y=$\frac{4}{3}$x-2=$\frac{10}{3}$,则P′(4,$\frac{10}{3}$),
综上所述,满足条件的P点坐标为(0,-2)或(3,2)或(4,$\frac{10}{3}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、一次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式;理解坐标与图形性质,记住两点间的距离公式;会运用勾股定理和相似比计算线段的长;能运用分类讨论的思想解决数学问题.

| A. | 2400名学生 | |
| B. | 100名学生 | |
| C. | 所抽取的100名学生对“白求恩同志事迹”的知晓情况 | |
| D. | 每一名学生对“白求恩同志事迹”的知晓情况 |
 如图,在菱形ABCD中,点O在对角线AC上,且AO=2CO,连接OB、OD,若OB=OC=OD,AC=3,则菱形的边长为( )
如图,在菱形ABCD中,点O在对角线AC上,且AO=2CO,连接OB、OD,若OB=OC=OD,AC=3,则菱形的边长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
①如果EF=AD,那么四边形AEDF是矩形
②如果EF⊥AD,那么四边形AEDF是菱形
③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形
其中正确的有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
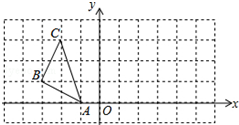 如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是( )
如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是( )| A. | (2,1) | B. | (1,2) | C. | (-2,-1) | D. | (-1,-2) |
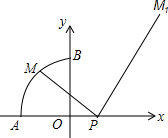 如图,点P(t,0)(t>0)是x轴正半轴上的一点,是以原点为圆心,半径为1的$\frac{1}{4}$圆,且A(-1,0),B(0,1),点M是$\widehat{AB}$上的一个动点,连结PM,作直角△MPM1,并使得∠MPM1=90°,∠PMM1=60°,我们称点M1为点M的对应点.
如图,点P(t,0)(t>0)是x轴正半轴上的一点,是以原点为圆心,半径为1的$\frac{1}{4}$圆,且A(-1,0),B(0,1),点M是$\widehat{AB}$上的一个动点,连结PM,作直角△MPM1,并使得∠MPM1=90°,∠PMM1=60°,我们称点M1为点M的对应点.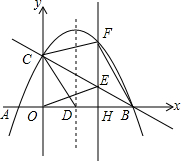 如图,抛物线y=-$\frac{1}{2}$x2+mx+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴直线x=$\frac{3}{2}$交x轴于点D.
如图,抛物线y=-$\frac{1}{2}$x2+mx+2与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴直线x=$\frac{3}{2}$交x轴于点D.