题目内容
3.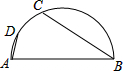 如图,AB是半圆的直径,D是弧AC的中点,∠ABC=50°,则∠DAB等于( )
如图,AB是半圆的直径,D是弧AC的中点,∠ABC=50°,则∠DAB等于( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
分析 连接AC,根据圆周角定理求出∠C的度数,故可得出∠BAC的度数,再由圆周角和弦的关系求出$\widehat{AC}$的度数,故可得出$\widehat{CD}$的度数,由此可得出结论.
解答 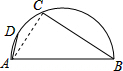 解:连接AC,
解:连接AC,
∵AB是半圆的直径,
∴∠C=90°.
∵∠ABC=50°,
∴∠BAC=90°-50°=40°,$\widehat{AC}$=50°,
∵D是弧AC的中点,
∴$\widehat{CD}$=25°,
∴∠DAC=25°,
∴∠DAB=∠DAC+∠BAC=25°+40°=65°.
故选C.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11. 如图,在菱形ABCD中,点O在对角线AC上,且AO=2CO,连接OB、OD,若OB=OC=OD,AC=3,则菱形的边长为( )
如图,在菱形ABCD中,点O在对角线AC上,且AO=2CO,连接OB、OD,若OB=OC=OD,AC=3,则菱形的边长为( )
 如图,在菱形ABCD中,点O在对角线AC上,且AO=2CO,连接OB、OD,若OB=OC=OD,AC=3,则菱形的边长为( )
如图,在菱形ABCD中,点O在对角线AC上,且AO=2CO,连接OB、OD,若OB=OC=OD,AC=3,则菱形的边长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
8.用配方法解一元二次方程x2-6x=-5的过程中,配方正确的是( )
| A. | (x+3)2=1 | B. | (x-3)2=1 | C. | (x+3)2=4 | D. | (x-3)2=4 |
15.在△ABC中,点D,E,F分别在BC,AB,CA上,且DE∥CA,DF∥BA,连接EF,则下列三种说法:
①如果EF=AD,那么四边形AEDF是矩形
②如果EF⊥AD,那么四边形AEDF是菱形
③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形
其中正确的有( )
①如果EF=AD,那么四边形AEDF是矩形
②如果EF⊥AD,那么四边形AEDF是菱形
③如果AD⊥BC且AB=AC,那么四边形AEDF是正方形
其中正确的有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
12.某校组织1080名学生去外地参观,现有A、B两种不同型号的客车可供选择.在每辆车刚好满座的前提下,每辆B型客车比每辆A型客车多坐15人,单独选择B型客车比单独选择A型客车少租12辆,设A型客车每辆坐x人,根据题意列方程为( )
| A. | $\frac{1080}{x}=\frac{1080}{x-15}+12$ | B. | $\frac{1080}{x}=\frac{1080}{x-15}-12$ | ||
| C. | $\frac{1080}{x}=\frac{1080}{x+15}-12$ | D. | $\frac{1080}{x}=\frac{1080}{x+15}+12$ |
13.计算(-2a3)2的结果是( )
| A. | -8a5 | B. | 4a6 | C. | 8a5 | D. | -4a6 |
 如图,四边形OABC的边OA,OC分别在y轴、x轴的正半轴,已知:A(0,4),B(4,3),C(4,0).
如图,四边形OABC的边OA,OC分别在y轴、x轴的正半轴,已知:A(0,4),B(4,3),C(4,0).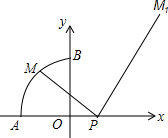 如图,点P(t,0)(t>0)是x轴正半轴上的一点,是以原点为圆心,半径为1的$\frac{1}{4}$圆,且A(-1,0),B(0,1),点M是$\widehat{AB}$上的一个动点,连结PM,作直角△MPM1,并使得∠MPM1=90°,∠PMM1=60°,我们称点M1为点M的对应点.
如图,点P(t,0)(t>0)是x轴正半轴上的一点,是以原点为圆心,半径为1的$\frac{1}{4}$圆,且A(-1,0),B(0,1),点M是$\widehat{AB}$上的一个动点,连结PM,作直角△MPM1,并使得∠MPM1=90°,∠PMM1=60°,我们称点M1为点M的对应点.