Question

3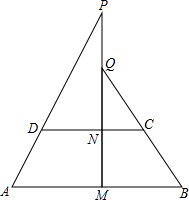．在四边形ABCD中，AD=BC，M、N分别是AB、CD的中点，MN所在的直线分别与AD、BC的延长线交于P、Q．求证：∠APM=∠BQM．

Answer 1

分析 连接AC，取AC中点G，连接NG、MG，根据中位线定理证明MG∥BC，且GM=$\frac{1}{2}$BC，根据AD=BC证明GM=GN，可得∠GNM=∠GMN，根据平行线性质可得：∠GMQ=∠MQB，∠GNM=∠P，从而得出∠APM=∠BQM．

解答 证明：连接AC，取AC中点G，连接NG、MG．
∵N是CD的中点，G是AC的中点，
∴NG=$\frac{1}{2}$AD，
又∵M是AB的中点，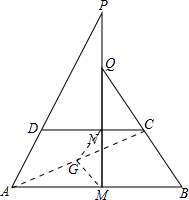
∴MG∥BC，且MG=$\frac{1}{2}$BC．
∵AD=BC，
∴NG=GM，
△GNM为等腰三角形，
∴∠GNM=∠GMN，
∵GM∥BF，
∴∠GMQ=∠MQB，
∵GN∥AD，
∴∠GNM=∠APM，
∴∠APM=∠BQM．

点评 此题主要考查平行线性质，以及三角形中位线定理，关键是证明△GNM为等腰三角形．