题目内容
6.用配方法解关于x的一元二次方程x2-2x-3=0,配方后的方程可以是( )| A. | (x+1)2=4 | B. | (x-1)2=4 | C. | (x-1)2=16 | D. | (x+1)2=16 |
分析 移项后两边都加上一次项系数一半的平方可得.
解答 解:∵x2-2x=3,
∴x2-2x+1=3+1,即(x-1)2=4,
故选:B.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
7.若分式$\frac{x+2}{x-1}$的值为0,则x的值为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
17.将一个圆分割成四个大小相同的扇形,则每个扇形的圆心角是( )度.
| A. | 45 | B. | 60 | C. | 90 | D. | 120 |
1.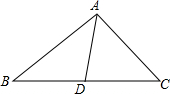 如图,在△ABC中,AB=7,BC边上的中线AD的长为5,则AC的长可能是( )
如图,在△ABC中,AB=7,BC边上的中线AD的长为5,则AC的长可能是( )
 如图,在△ABC中,AB=7,BC边上的中线AD的长为5,则AC的长可能是( )
如图,在△ABC中,AB=7,BC边上的中线AD的长为5,则AC的长可能是( )| A. | 3 | B. | 10 | C. | 17 | D. | 20 |
11.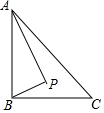 如图,Rt△ABC中,AB⊥BC,AB=10,BC=12,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
如图,Rt△ABC中,AB⊥BC,AB=10,BC=12,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
 如图,Rt△ABC中,AB⊥BC,AB=10,BC=12,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
如图,Rt△ABC中,AB⊥BC,AB=10,BC=12,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )| A. | 7 | B. | 8 | C. | $\frac{8\sqrt{13}}{13}$ | D. | $\frac{12\sqrt{13}}{13}$ |
18.一个不透明的袋子装有3个小球,它们除分别标有的数字1,3,5不同外,其他完全相同,任意从袋子中摸出一球后放回,再任意摸出一球,则两次摸出的球所标数字之和为6的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
 如图,是一个正方体的平面展开图,把展开图折叠成正方体后“美”字一面相对的字是京.
如图,是一个正方体的平面展开图,把展开图折叠成正方体后“美”字一面相对的字是京.