题目内容
14.小金到都江堰的距离约为180km,小刘开着小轿车,小张开着大货车,都从小金去都江堰,小刘比小张晚出发1小时,最后两车同时到达都江堰,已知小轿车的速度是大货车速度的1.5倍.(1)求小轿车和大货车的速度各是多少?(列方程解答)
(2)当小刘出发时,求小张离都江堰还有多远?
分析 (1)设大货车速度为xkm/时,则小轿车的速度是1.5xkm/时,方程为$\frac{180}{x}$-$\frac{180}{1.5x}$=1,求出方程的解即可;
(2)根据题意列出算式,求出即可.
解答 解:(1)设大货车速度为xkm/时,则小轿车的速度是1.5xkm/时,
$\frac{180}{x}$-$\frac{180}{1.5x}$=1,
解得:x=60,
经检验x=60是所列方程的解,
1.5x=75,
答:大货车速度为60km/时,则小轿车的速度是75km/时;
(2)180-60×1=120,
答:当小刘出发时,求小张离都江堰还有120km.
点评 本题考查了分式方程的应用,能根据相等关系列出方程是解此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
9.若$\frac{b}{a}$有意义,m≠0,则下面结论中成立的是( )
| A. | $\frac{b+m}{a+m}=\frac{b}{a}$ | B. | $\frac{b-m}{a-m}=\frac{b}{a}$ | C. | $\frac{-bm}{-am}=\frac{b}{a}$ | D. | $\frac{mb}{a}=\frac{b}{a}$ |
19.已知4n-m=4,则(m-4n)2-3(m-4n)-10的值是( )
| A. | -6 | B. | 6 | C. | 18 | D. | -38 |
6.用配方法解关于x的一元二次方程x2-2x-3=0,配方后的方程可以是( )
| A. | (x+1)2=4 | B. | (x-1)2=4 | C. | (x-1)2=16 | D. | (x+1)2=16 |
4.下列实数中是无理数的是( )
| A. | -$\sqrt{3}$ | B. | -$\frac{2}{3}$ | C. | 0 | D. | 3.14 |
 太阳能光伏发电是一种清洁、安全、便利、高效的新兴能源,因而逐渐被推广使用.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,支撑角钢EF长为$\frac{{290\sqrt{3}}}{3}$cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,FE⊥AB于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为 30cm,点A到地面的垂直距离为50cm,则支撑角钢CD的长度是45cm,AB的长度是300cm.
太阳能光伏发电是一种清洁、安全、便利、高效的新兴能源,因而逐渐被推广使用.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,支撑角钢EF长为$\frac{{290\sqrt{3}}}{3}$cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,FE⊥AB于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为 30cm,点A到地面的垂直距离为50cm,则支撑角钢CD的长度是45cm,AB的长度是300cm.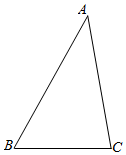 如图,在△ABC中,BC=3$\sqrt{2}$,AC=5,∠B=45°,则下面结论正确的是①③④.
如图,在△ABC中,BC=3$\sqrt{2}$,AC=5,∠B=45°,则下面结论正确的是①③④.