题目内容
15.如果∠1与∠2互为余角,∠1与∠3互为补角,那么下列结论:①∠3-∠2=90° ②∠3+∠2=270°-2∠1 ③∠3-∠1=2∠2 ④∠3>∠1+∠2.
正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据互余的两角之和为90°,互补的两角之和为180°即可求解.
解答 解:∵∠1与∠2互为余角,∠1与∠3互为补角,
∴∠1+∠2=90°,∠1+∠3=180°,
∴①∠3-∠2=90° 是正确的;
②∠3+∠2=270°-2∠1是正确的;
③∠3-∠1=2∠2 是正确的;
④∠3=∠1+2∠2,即∠3>∠1+∠2是正确的.
故选:D.
点评 本题考查了余角和补角的知识,解答本题的关键是掌握互余的两角之和为90°,互补的两角之和为180°.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
6.用配方法解关于x的一元二次方程x2-2x-3=0,配方后的方程可以是( )
| A. | (x+1)2=4 | B. | (x-1)2=4 | C. | (x-1)2=16 | D. | (x+1)2=16 |
20.下列四个数中,最大的数是( )
| A. | 1 | B. | 0 | C. | |-2| | D. | -3 |
4.下列实数中是无理数的是( )
| A. | -$\sqrt{3}$ | B. | -$\frac{2}{3}$ | C. | 0 | D. | 3.14 |
5.下列命题是真命题的是( )
| A. | 如果|a|=1,那么a=1 | |
| B. | 三个内角分别对应相等的两个三角形全等 | |
| C. | 如果a是有理数,那么a是实数 | |
| D. | 两边一角对应相等的两个三角形全等 |
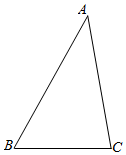 如图,在△ABC中,BC=3$\sqrt{2}$,AC=5,∠B=45°,则下面结论正确的是①③④.
如图,在△ABC中,BC=3$\sqrt{2}$,AC=5,∠B=45°,则下面结论正确的是①③④. 如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,且横、竖彩条的宽度相等,如果要使彩条所占面积为184cm2,应如何设计彩条的宽度?
如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,且横、竖彩条的宽度相等,如果要使彩条所占面积为184cm2,应如何设计彩条的宽度?