题目内容
14.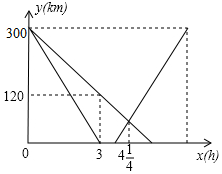 某客运公司的特快巴士与普通巴士同时从甲地出发,以各自的速度匀速向乙地行驶,普通巴士到达乙地后停止,特快巴士到达乙地停留45分钟后,按原路以另一速度匀速返回甲地,已知两辆巴士分别距乙地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示.求普通巴士到达乙地时,特快巴士与甲地之间的距离为187.5千米.
某客运公司的特快巴士与普通巴士同时从甲地出发,以各自的速度匀速向乙地行驶,普通巴士到达乙地后停止,特快巴士到达乙地停留45分钟后,按原路以另一速度匀速返回甲地,已知两辆巴士分别距乙地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示.求普通巴士到达乙地时,特快巴士与甲地之间的距离为187.5千米.
分析 首先求出两车的速度,普通巴士的函数解析式,求出两车相遇时离乙地的路程,再求出普通巴士相遇后到目的地的时间,求出特快巴士返回离乙地的路程,即可解决问题.
解答 解:设普通巴士的函数解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=300}\\{3k+b=120}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-60}\\{b=300}\end{array}\right.$,
∴y=-60x+300,
当x=4$\frac{1}{4}$时,y=45,
∴特快巴士去时的速度为100km/h,返回时是速度为$\frac{45}{\frac{1}{2}}$=90km/h,
普通巴士的速度为$\frac{180}{3}$=60km/h,
两车相遇后又走了$\frac{45}{60}$=$\frac{3}{4}$h到目的地,
∵90×($\frac{1}{2}$+$\frac{3}{4}$)=112.5km,
300-112.5=187.5km,
∴普通巴士到达乙地时,特快巴士与甲地之间的距离为187.5km.
故答案为187.5.
点评 本题考查一次函数的应用,路程、速度、时间之间的关系等知识,解题的关键是理解题意,学会读懂图象信息,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
19.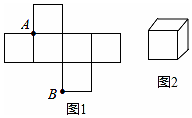 如图1是边长为1的六个小正方形组成的平面图形,将它围成图2的正方体,则图1中小正方形顶点A,B在围成的正方体上的距离是( )
如图1是边长为1的六个小正方形组成的平面图形,将它围成图2的正方体,则图1中小正方形顶点A,B在围成的正方体上的距离是( )
 如图1是边长为1的六个小正方形组成的平面图形,将它围成图2的正方体,则图1中小正方形顶点A,B在围成的正方体上的距离是( )
如图1是边长为1的六个小正方形组成的平面图形,将它围成图2的正方体,则图1中小正方形顶点A,B在围成的正方体上的距离是( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 0 |
6. a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
 a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )| A. | 2a-b | B. | b | C. | -b | D. | -2a+b |
3.观察下列图形,第1个图形中平行四边形有1个,第2个图形中平行四边形有5个,第3个图形中平行四边形有11个,…,依此类推,第6个图形中平行四边形有( )
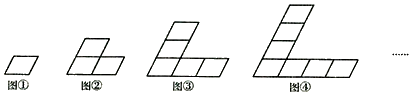

| A. | 29个 | B. | 41个 | C. | 45个 | D. | 55个 |
4.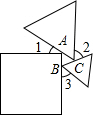 如图,一个正方形和两个等边三角形的位置如图所示,若∠2=50°,则∠1+∠3=( )
如图,一个正方形和两个等边三角形的位置如图所示,若∠2=50°,则∠1+∠3=( )
 如图,一个正方形和两个等边三角形的位置如图所示,若∠2=50°,则∠1+∠3=( )
如图,一个正方形和两个等边三角形的位置如图所示,若∠2=50°,则∠1+∠3=( )| A. | 90° | B. | 100° | C. | 130° | D. | 180° |
