题目内容
2. 如图,在边长为$2\sqrt{3}$的等边三角形ABC中,以点A为圆心的圆与边BC相切,与边AB、AC相交于点D、E,则图中阴影部分的面积为$3\sqrt{3}-\frac{3}{2}π$.
如图,在边长为$2\sqrt{3}$的等边三角形ABC中,以点A为圆心的圆与边BC相切,与边AB、AC相交于点D、E,则图中阴影部分的面积为$3\sqrt{3}-\frac{3}{2}π$.
分析 首先求得圆的半径,根据阴影部分的面积=△ABC的面积-扇形ADE的面积即可求解.
解答 解:设以点A为圆心的圆与边BC相切于点F,连接AF,如图所示:
则AF⊥BC,
∵△ABC是等边三角形,
∴∠B=60°,BC=AB=2$\sqrt{3}$,
∴AF=AB•sin60°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,
∴阴影部分的面积=△ABC的面积-扇形ADE的面积=$\frac{1}{2}$×2$\sqrt{3}$×3-$\frac{60π×{3}^{2}}{360}$=3$\sqrt{3}$-$\frac{3}{2}$π.
故答案为:$3\sqrt{3}-\frac{3}{2}π$.
点评 本题主要考查了扇形的面积的计算、三角函数、切线的性质、等边三角形的性质;熟练掌握切线的性质,由三角函数求出AF是解决问题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
10.下列计算正确的是( )
| A. | 4x6÷(2x2)=2x3 | B. | 30=0 | C. | 3-1=-3 | D. | x${\;}^{-2}=\frac{1}{{x}^{2}}$ |

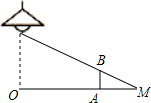 如图,身高1.6米的小明站在距离灯的底部(点O)20米的A处,经测量小明的影子AM长为5米,则路灯的高度为8米.
如图,身高1.6米的小明站在距离灯的底部(点O)20米的A处,经测量小明的影子AM长为5米,则路灯的高度为8米.