题目内容
17.求下列各式的值(1)$\frac{{3+2a-{a^2}}}{{{a^2}-7a+12}}$,其中a=-2.
(2)$\frac{{{x^2}-3xy-18{y^2}}}{{{x^2}-5xy-6{y^2}}}$,其中x=-3,y=1.
分析 (1)原式变形后,约分得到最简结果,把a的值代入计算即可求出值;
(2)原式约分得到最简结果,把x与y的值代入计算即可求出值.
解答 解:(1)原式=$\frac{-({a}^{2}-2a-3)}{{a}^{2}-7a+12}$=-$\frac{(a-3)(a+1)}{(a-3)(a-4)}$=-$\frac{a+1}{a-4}$,
当a=-2时,原式=-$\frac{-2+1}{-2-4}$=$\frac{1}{6}$;
(2)原式=$\frac{(x-6y)(x+3y)}{(x-6y)(x+y)}$=$\frac{x+3y}{x+y}$,
当x=-3,y=1时,原式=0.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )
数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )
 数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )
数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
12.下列四个命题中,假命题是( )
| A. | 两角对应相等,两个三角形相似 | |
| B. | 三边对应成比例,两个三角形相似 | |
| C. | 两边对应成比例且其中一边的对角相等,两个三角形相似 | |
| D. | 两边对应成比例且夹角相等,两个三角形相似 |
 有增根,则m的值为____________.
有增根,则m的值为____________. 如图,在边长为$2\sqrt{3}$的等边三角形ABC中,以点A为圆心的圆与边BC相切,与边AB、AC相交于点D、E,则图中阴影部分的面积为$3\sqrt{3}-\frac{3}{2}π$.
如图,在边长为$2\sqrt{3}$的等边三角形ABC中,以点A为圆心的圆与边BC相切,与边AB、AC相交于点D、E,则图中阴影部分的面积为$3\sqrt{3}-\frac{3}{2}π$.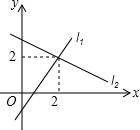 如图,直线l1:y=k1x+b1与直线l2:y=k2x+b2交于点(2,2),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
如图,直线l1:y=k1x+b1与直线l2:y=k2x+b2交于点(2,2),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.