题目内容
14.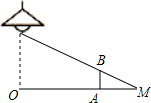 如图,身高1.6米的小明站在距离灯的底部(点O)20米的A处,经测量小明的影子AM长为5米,则路灯的高度为8米.
如图,身高1.6米的小明站在距离灯的底部(点O)20米的A处,经测量小明的影子AM长为5米,则路灯的高度为8米.
分析 根据题意得出:△COM∽△BAM,进而利用相似三角形的性质得出路灯的高度.
解答  解:由题意可得:△COM∽△BAM,
解:由题意可得:△COM∽△BAM,
则$\frac{AM}{OM}$=$\frac{AB}{CO}$,
故$\frac{5}{5+20}$=$\frac{1.6}{CO}$,
解得:CO=8.
故答案为:8.
点评 本题考查了相似三角形的应用;在运用相似三角形的知识解决实际问题时,要能够从实际问题中抽象出简单的数学模型是解决问题的关键.

练习册系列答案
相关题目
19.计算:(-12)+(+$\frac{6}{5}$)+(-8)+(-$\frac{7}{10}$)+(-$\frac{1}{2}$)=( )
| A. | -19 | B. | -18 | C. | -20 | D. | -17 |
3.下表中的字母都是按移动规律排列的.
我们把某格中的字母的和所得多项式称为特征多项式,例如第1格的“特征多项式”为6x+2y,第2格的“特征多项式”为9x+4y,回答下列问题.
(1)第3格的“特征多项式”为12x+6y,第4格的“特征多项式”为15x+8y,第n格的“特征多项式”为3(n+1)x+2ny(n为正整数);
(2)求第6格的“特征多项式”与第5格的“特征多项式”的差.
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x | … |
(1)第3格的“特征多项式”为12x+6y,第4格的“特征多项式”为15x+8y,第n格的“特征多项式”为3(n+1)x+2ny(n为正整数);
(2)求第6格的“特征多项式”与第5格的“特征多项式”的差.
 有个零件(正方体中间挖去一个圆柱形孔)如图放置,它的左视图是( )
有个零件(正方体中间挖去一个圆柱形孔)如图放置,它的左视图是( )



 如图,在边长为$2\sqrt{3}$的等边三角形ABC中,以点A为圆心的圆与边BC相切,与边AB、AC相交于点D、E,则图中阴影部分的面积为$3\sqrt{3}-\frac{3}{2}π$.
如图,在边长为$2\sqrt{3}$的等边三角形ABC中,以点A为圆心的圆与边BC相切,与边AB、AC相交于点D、E,则图中阴影部分的面积为$3\sqrt{3}-\frac{3}{2}π$.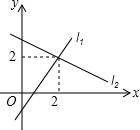 如图,直线l1:y=k1x+b1与直线l2:y=k2x+b2交于点(2,2),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
如图,直线l1:y=k1x+b1与直线l2:y=k2x+b2交于点(2,2),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.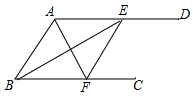 如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证:
如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证: