题目内容
5.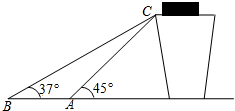 某货站传送货物的平面示意图如图所示,为了提高传送过程的安全性,工人师傅欲减少传送带与地面的夹角,使其由45°变为37°,因此传送带的落地点A到点B向前移动了2米.求货物(即点C)到地面的高度.(结果精确到0.1米)
某货站传送货物的平面示意图如图所示,为了提高传送过程的安全性,工人师傅欲减少传送带与地面的夹角,使其由45°变为37°,因此传送带的落地点A到点B向前移动了2米.求货物(即点C)到地面的高度.(结果精确到0.1米)【参考数据:sin37°=0.6018,cos37°=0.7986,tan37°=0.7536】
分析 首先过点C作CD⊥AB于点D,则∠ADC=∠BDC=90°,然后分别在Rt△ACD中与在Rt△BCD中,表示出AD,BD与CD的关系,继而列出方程:$\frac{CD}{0.7536}$-CD=2,解此方程即可求得答案.
解答 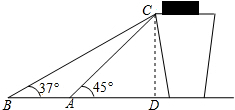 解:过点C作CD⊥AB于点D,则∠ADC=∠BDC=90°,
解:过点C作CD⊥AB于点D,则∠ADC=∠BDC=90°,
在Rt△ACD中,∠CAD=45°,
∴CD=AD,
在Rt△BCD中,∠CBD=37°,tan∠CBD=$\frac{CD}{BD}$,
∴BD=$\frac{CD}{tan37°}$,
∵AB=BD-AD=2,
∴$\frac{CD}{0.7536}$-CD=2,
解得:CD=$\frac{471}{77}$≈6.1(米).
答:货物(即点C)到地面的高度为6.1米.
点评 此题考查了坡度坡角问题.注意准确构造直角三角形是关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
13.要使函数y=$\sqrt{x-1}$有意义,自变量x的取值范围是( )
| A. | x≥1 | B. | x≤1 | C. | x>1 | D. | x<1 |
20.一元二次方程x2-4x+6=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
10.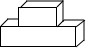 如图,观察这个立体图形,它的俯视图是( )
如图,观察这个立体图形,它的俯视图是( )
 如图,观察这个立体图形,它的俯视图是( )
如图,观察这个立体图形,它的俯视图是( )| A. |  | B. | 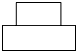 | C. |  | D. |  |
 甲乙两人玩纸牌游戏,如图是同一副扑克中的4张扑克牌的正面,将它们正面朝下后放在桌上,甲先从中抽出一张,乙从剩余的3张牌中也抽出一张.
甲乙两人玩纸牌游戏,如图是同一副扑克中的4张扑克牌的正面,将它们正面朝下后放在桌上,甲先从中抽出一张,乙从剩余的3张牌中也抽出一张. 按如图方式折叠一张对边互相平行的纸条,EF是折痕,若∠EFB=32°,则
按如图方式折叠一张对边互相平行的纸条,EF是折痕,若∠EFB=32°,则