题目内容
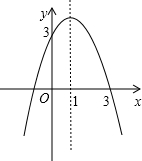 已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题:
已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题:(1)关于x的一元二次方程-x2+bx+c=0的解为
(2)求此抛物线的解析式;
(3)当x为值时,y<0;
(4)若直线y=k与抛物线没有交点,直接写出k的范围.
考点:抛物线与x轴的交点,二次函数的图象,待定系数法求二次函数解析式,二次函数与不等式(组)
专题:
分析:(1)直接观察图象,抛物线与x轴交于-1,3两点,所以方程的解为x1=-1,x2=3.
(2)设出抛物线的顶点坐标形式,代入坐标(3,0),即可求得抛物线的解析式.
(3)若y<0,则函数的图象在x轴的下方,找到对应的自变量取值范围即可.
(4)若直线y=k与抛物线没有交点,则k>函数的最大值即可.
(2)设出抛物线的顶点坐标形式,代入坐标(3,0),即可求得抛物线的解析式.
(3)若y<0,则函数的图象在x轴的下方,找到对应的自变量取值范围即可.
(4)若直线y=k与抛物线没有交点,则k>函数的最大值即可.
解答:解:(1)观察图象可看对称轴出抛物线与x轴交于x=-1和x=3两点,
∴方程的解为x1=-1,x2=3,
故答案为:-1或3;
(2)设抛物线解析式为y=-(x-1)2+k,
∵抛物线与x轴交于点(3,0),
∴(3-1)2+k=0,
解得:k=4,
∴抛物线解析式为y=-(x-1)2+4,
即:抛物线解析式为y=-x2+2x+3;
(3)若y<0,则函数的图象在x轴的下方,由函数的图象可知:x>3或x<-1;
(4)若直线y=k与抛物线没有交点,则k>函数的最大值,即y>4.
∴方程的解为x1=-1,x2=3,
故答案为:-1或3;
(2)设抛物线解析式为y=-(x-1)2+k,

∵抛物线与x轴交于点(3,0),
∴(3-1)2+k=0,
解得:k=4,
∴抛物线解析式为y=-(x-1)2+4,
即:抛物线解析式为y=-x2+2x+3;
(3)若y<0,则函数的图象在x轴的下方,由函数的图象可知:x>3或x<-1;
(4)若直线y=k与抛物线没有交点,则k>函数的最大值,即y>4.
点评:本题考查了用待定系数法求函数解析式的方法,同时还考查了方程组的解法等知识,难度不大.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 如图,给出下列条件:①∠3=∠4;②∠1=∠2;③EF∥CD,且∠D=∠4;④∠3+∠5=180°.其中,能推出AD∥BC的条件为( )
如图,给出下列条件:①∠3=∠4;②∠1=∠2;③EF∥CD,且∠D=∠4;④∠3+∠5=180°.其中,能推出AD∥BC的条件为( )| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
 如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则sin∠B′的值为( )
如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则sin∠B′的值为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
 如图,△ABC中,AB=AC,∠BAC=70°,P为BC上一点,将△ABP绕点A按逆时针方向旋转到△ACP′位置,则∠AP′P的度数为( )
如图,△ABC中,AB=AC,∠BAC=70°,P为BC上一点,将△ABP绕点A按逆时针方向旋转到△ACP′位置,则∠AP′P的度数为( )| A、30° | B、60° |
| C、45° | D、55° |
 如图,⊙O中,弦AB垂直平分半径OC,垂足为P,若AB=6,则⊙O半径为
如图,⊙O中,弦AB垂直平分半径OC,垂足为P,若AB=6,则⊙O半径为 某中学举行的科普知识竞赛中,将初三四个班级的参赛学生的成绩(得分均为正整数)进行整理后分成五组,绘制出图如下.从左到右的第二小组的频率是0.4.
某中学举行的科普知识竞赛中,将初三四个班级的参赛学生的成绩(得分均为正整数)进行整理后分成五组,绘制出图如下.从左到右的第二小组的频率是0.4. 已知:如图,AE∥BF,AC平分∠BAD,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
已知:如图,AE∥BF,AC平分∠BAD,交BF于点C,BD平分∠ABC,交AE于点D,连接CD. 如图,已知直线y=kx+b经过(2,-1)和(-1,2),且与两坐标轴交于A、B两点,求不等式kx+b≥0的解集.
如图,已知直线y=kx+b经过(2,-1)和(-1,2),且与两坐标轴交于A、B两点,求不等式kx+b≥0的解集.