题目内容
 如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则sin∠B′的值为( )
如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则sin∠B′的值为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
考点:旋转的性质,勾股定理,锐角三角函数的定义
专题:网格型
分析:如图在Rt△BCD中,由CD=1,BD=3,根据勾股定理可计算出BC=
,再根据正弦的定义得到sinB=
=
=
,然后根据旋转的性质得∠B′=∠B,则有sinB′=sinB=
.
| 10 |
| CD |
| BC |
| 1 | ||
|
| ||
| 10 |
| ||
| 10 |
解答:解:如图, 设正方形网格中每个小正方形的边长为1,
设正方形网格中每个小正方形的边长为1,
在Rt△BCD中,∵CD=1,BD=3,
∴BC=
=
=
,
∴sinB=
=
=
,
∵△ABC绕着点A逆时针旋转得到△AC′B′,
∴∠B′=∠B,
∴sinB′=
.
故选B.
 设正方形网格中每个小正方形的边长为1,
设正方形网格中每个小正方形的边长为1,在Rt△BCD中,∵CD=1,BD=3,
∴BC=
| BD2+CD2 |
| 32+12 |
| 10 |
∴sinB=
| CD |
| BC |
| 1 | ||
|
| ||
| 10 |
∵△ABC绕着点A逆时针旋转得到△AC′B′,
∴∠B′=∠B,
∴sinB′=
| ||
| 10 |
故选B.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了勾股定理以及三角形函数的定义.

练习册系列答案
相关题目
 如图,△ABC为等边三角形,BD=DE,∠BDE=120°,连接CE,F为CE的中点,连接DF并倍长,连接AD、CG、AG.下列结论:
如图,△ABC为等边三角形,BD=DE,∠BDE=120°,连接CE,F为CE的中点,连接DF并倍长,连接AD、CG、AG.下列结论:①CG=DE;②若DE∥BC,则△ABH∽△GBD;③在②的条件下,若CE⊥BC,则
| AD |
| BD |
| ||
| 2 |
其中正确的有( )
| A、①②③都正确 |
| B、只有①②正确 |
| C、只有②③正确 |
| D、只有①③正确 |
 ①如图,线段AB与A1B1关于某点对称,请在图中画出这个点并写出这个点的坐标.
①如图,线段AB与A1B1关于某点对称,请在图中画出这个点并写出这个点的坐标.
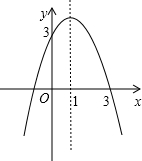 已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题:
已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题: