题目内容
7.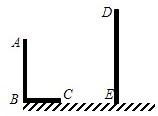 如图,AB和DE是直立在地面上的两根立柱.AB=4m,某一时刻AB在阳光下的投影BC=3m.
如图,AB和DE是直立在地面上的两根立柱.AB=4m,某一时刻AB在阳光下的投影BC=3m.(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8m,请你计算DE的长.
分析 (1)根据投影的定义,作出投影即可;
(2)根据在同一时刻,不同物体的物高和影长成比例;构造比例关系AB:DE=BC:EF.计算可得DE=10(m).
解答  解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
(2)∵AC∥DF,
∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°
∴△ABC∽△DEF.
∴AB:DE=BC:EF,
∵AB=4m,BC=3m,EF=8
∴4:3=DE:8
∴DE=$\frac{32}{3}$(m).
点评 本题考查了平行投影特点:在同一时刻,不同物体的物高和影长成比例.要求学生通过投影的知识并结合图形解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.一元一次方程-2x=4的解是( )
| A. | x=-2 | B. | x=2 | C. | x=1 | D. | x=-$\frac{1}{2}$ |
18.若一个三角形三个内角度数的比为2:3:4,则这个三角形是( )
| A. | 直角三角形 | B. | 等边三角形 | C. | 钝角三角形 | D. | 锐角三角形 |
15. 某鲜花销售部在春节前20天内销售一批鲜花.其中,该销售部公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)关系为二次函数,部分对应值如表所示.
某鲜花销售部在春节前20天内销售一批鲜花.其中,该销售部公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)关系为二次函数,部分对应值如表所示.
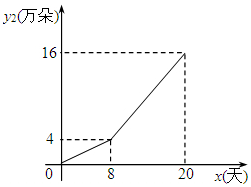
与此同时,该销售部还通过某网络电子商务平台销售鲜花,网上销售日销售量y2(万朵)与时间x(x为整数,单位:天) 的函数关系如图所示.
(1)求y1与x的二次函数关系式及自变量x的取值范围;
(2)求y2与x的函数关系式及自变量x的取值范围;
(3)当8≤x≤20时,设该花木公司鲜花日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时的最大值.
 某鲜花销售部在春节前20天内销售一批鲜花.其中,该销售部公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)关系为二次函数,部分对应值如表所示.
某鲜花销售部在春节前20天内销售一批鲜花.其中,该销售部公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)关系为二次函数,部分对应值如表所示.| 时间x(天) | 0 | 4 | 8 | 12 | 16 | 20 |
| 销量y1(万朵) | 0 | 16 | 24 | 24 | 16 | 0 |
(1)求y1与x的二次函数关系式及自变量x的取值范围;
(2)求y2与x的函数关系式及自变量x的取值范围;
(3)当8≤x≤20时,设该花木公司鲜花日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时的最大值.
2.小红同学四次数学测试成绩分别是:96,104,104,116,关于这组数据下列说法错误的是( )
| A. | 平均数是105 | B. | 众数是104 | C. | 中位数是104 | D. | 方差是50 |
19.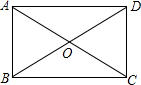 如图,矩形ABCD中,AB=1,∠AOB=60°,则BC=( )
如图,矩形ABCD中,AB=1,∠AOB=60°,则BC=( )
 如图,矩形ABCD中,AB=1,∠AOB=60°,则BC=( )
如图,矩形ABCD中,AB=1,∠AOB=60°,则BC=( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
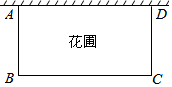 为了美化生活环境,小明的爸爸要在院墙外的一块空地上修建一个矩形花圃.如图所示,矩形花圃的一边利用长10米的院墙,另外三条边用篱笆围成,篱笆的总长为32米.设AB的长为x米,矩形花圃的面积为y平方米.
为了美化生活环境,小明的爸爸要在院墙外的一块空地上修建一个矩形花圃.如图所示,矩形花圃的一边利用长10米的院墙,另外三条边用篱笆围成,篱笆的总长为32米.设AB的长为x米,矩形花圃的面积为y平方米.