题目内容
16.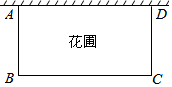 为了美化生活环境,小明的爸爸要在院墙外的一块空地上修建一个矩形花圃.如图所示,矩形花圃的一边利用长10米的院墙,另外三条边用篱笆围成,篱笆的总长为32米.设AB的长为x米,矩形花圃的面积为y平方米.
为了美化生活环境,小明的爸爸要在院墙外的一块空地上修建一个矩形花圃.如图所示,矩形花圃的一边利用长10米的院墙,另外三条边用篱笆围成,篱笆的总长为32米.设AB的长为x米,矩形花圃的面积为y平方米.(1)用含有x的代数式表示BC的长,BC=32-2x;
(2)求y与x的函数关系式,写出自变量x的取值范围;
(3)当x为何值时,y有最大值?
分析 (1)根据题意可以用含x的代数式表示出BC的长;
(2)根据题意可以得到y与x的函数关系式,并求出自变量x的取值范围;
(3)将(2)中函数关系式化为顶点式,然后根据x的取值范围即可解答本题.
解答 解:(1)由题意可得,
BC=32-2x,
故答案为:32-2x;
(2)由题意可得,
y=x(32-2x)=-2x2+32x,
∵$\left\{\begin{array}{l}{32-2x>0}\\{32-2x≤10}\end{array}\right.$,
∴11≤x<16,
即y与x的函数关系式是y=-2x2+32x(11≤x<16);
(3)∵y=-2x2+32x=-2(x-8)2+128,11≤x<16,
∴x=11时,y取得最大值,此时y=110,
即当x=11时,y取得最大值.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
11.七年级(1)班有x人,七年级(2)班人数比七年级(1)班的$\frac{3}{4}$多1人,则七年级(2)班的人数是( )
| A. | $\frac{3}{4}$x+1 | B. | $\frac{3x+1}{4}$ | C. | $\frac{3}{4}$x-1 | D. | $\frac{3}{4}$(x-1) |
8.已知点A(1,a)与点B(3,b)都在反比例函数y=-$\frac{12}{x}$的图象上,则a与b之间的关系是( )
| A. | a>b | B. | a<b | C. | a≥b | D. | a=b |
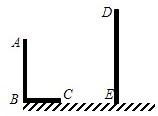 如图,AB和DE是直立在地面上的两根立柱.AB=4m,某一时刻AB在阳光下的投影BC=3m.
如图,AB和DE是直立在地面上的两根立柱.AB=4m,某一时刻AB在阳光下的投影BC=3m.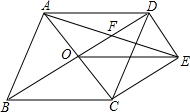 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE.
如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE.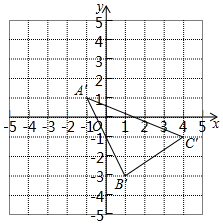 在平面直角坐标系中,A,B,C三点的坐标分别为(-5,4),(-3,0),(0,2).
在平面直角坐标系中,A,B,C三点的坐标分别为(-5,4),(-3,0),(0,2).