题目内容
11.通分:(1)-$\frac{5}{6{x}^{2}}$和$\frac{3}{4xyz}$;
(2)$\frac{1}{xy-{y}^{2}}$和$\frac{x+y}{{y}^{2}-{x}^{2}}$.
分析 (1)将两式系数取各系数的最小公倍数,相同因式的次数取最高次幂,即可得出答案.
(2)先把分母进行因式分解,再进行通分即可.
解答 解:(1)-$\frac{5}{6{x}^{2}}$=-$\frac{10yz}{12{x}^{2}yz}$,$\frac{3}{4xyz}$=$\frac{9x}{12{x}^{2}yz}$;
(2)$\frac{1}{xy-{y}^{2}}$=$\frac{1}{y(x-y)}$=-$\frac{y+x}{y(y-x)(y+x)}$,$\frac{x+y}{{y}^{2}-{x}^{2}}$=$\frac{y(x+y)}{y(y-x)(y+x)}$.
点评 此题考查了通分,解答此题的关键是熟知找公分母的方法:
(1)系数取各系数的最小公倍数;
(2)凡出现的因式都要取;
(3)相同因式的次数取最高次幂.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
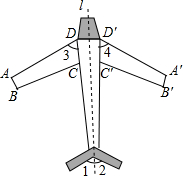 如图是轴对称图形.图中直线1是它的对称轴.
如图是轴对称图形.图中直线1是它的对称轴. 如图,在边长为2的正方形ABCD中,分别以各顶点为圆心,在正方形内作四条圆弧,使它们所在的圆外切于点E,F,G,H.则图中阴影部分的外围的周长是2π.(结果保留π)
如图,在边长为2的正方形ABCD中,分别以各顶点为圆心,在正方形内作四条圆弧,使它们所在的圆外切于点E,F,G,H.则图中阴影部分的外围的周长是2π.(结果保留π) 如图,圆柱的体积V=Sh.其中,S为圆柱的底而积,h为圆柱的高.
如图,圆柱的体积V=Sh.其中,S为圆柱的底而积,h为圆柱的高.