��Ŀ����
9��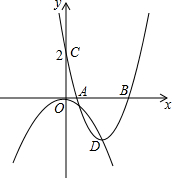 ��ͼ����֪������C1��y=-$\frac{1}{2}$x2��ƽ��������y=x2��ʹ�䶥��D����������C1λ��y���Ҳ��ͼ���ϣ���ƽ�ƺ��������ΪC2����C2��y�ύ�ڵ�C��0��2����
��ͼ����֪������C1��y=-$\frac{1}{2}$x2��ƽ��������y=x2��ʹ�䶥��D����������C1λ��y���Ҳ��ͼ���ϣ���ƽ�ƺ��������ΪC2����C2��y�ύ�ڵ�C��0��2������1����������C2�Ľ���ʽ��
��2��������C2��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ�����A��B�����꼰����A��B��C��Բ��Բ��E�����ꣻ
��3���ڹ��㣨0��$\frac{1}{2}$����ƽ����x���ֱ�����Ƿ���ڵ�F��ʹ�ı���CEBFΪ���Σ������ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
���� ��1����D��a��-$\frac{1}{2}$a2�����������a��ֵ�ó���������ʽ���ɣ�
��2������y=0���A��B�����꣬������|CE|=|AE|�����m��ֵ�����ó��𰸣�
��3���������ε����ʽ��|BF|=|CF|=|CE|�������|FC|�������ó��𰸣�
���  �⣺��1����������D��a��-$\frac{1}{2}$a2����
�⣺��1����������D��a��-$\frac{1}{2}$a2����
����������C2�Ľ���ʽΪ��y=��x-a��2-$\frac{1}{2}$a2��
�ߵ�C��������C2�ϣ�
�ཫC��0��2��������ʽ��
��ã�a=��2��
�ߵ�D��y���Ҳ࣬
��a=2��
��������C2�Ľ���ʽΪ��y=��x-2��2-2��
��2�������⣬��y=��x-2��2-2�У���y=0����x=2��$\sqrt{2}$��
�ߵ�B�ڵ�A���Ҳ࣬
��A��2-$\sqrt{2}$��0����B��2+$\sqrt{2}$��0����
�֡߹���A��B��C��Բ��Բ��һ�����߶�AB�Ĵ�ֱƽ�����ϣ�
����E��2��m������|CE|=|AE|��
��22+��2-m��2=m2+��2-2+$\sqrt{2}$��2��
��ã�m=$\frac{3}{2}$��
��Բ��E������Ϊ����2��$\frac{3}{2}$����
��3��������ڵ�F��t��$\frac{1}{2}$����ʹ���ı���CEBFΪ���Σ�
��|BF|=|CF|=|CE|��
�ࣨ$\frac{1}{2}$��2+��2+$\sqrt{2}$-t��2=��2-$\frac{1}{2}$��2+t2��
��ã�t=$\sqrt{2}$��
��t=$\sqrt{2}$ʱ��F��2��$\frac{1}{2}$����
��ʱ|EC|=$\frac{\sqrt{17}}{2}$��
|FC|=$\sqrt{��\sqrt{2}��^{2}+��2-\frac{1}{2}��^{2}}$=$\sqrt{2+\frac{9}{4}}$=$\frac{\sqrt{17}}{2}$��
��|CF|=|BF|=|BE|=|EC|��
�����ڵ�F��$\sqrt{2}$��$\frac{1}{2}$����ʹ���ı���CEBFΪ���Σ�
���� ������Ҫ�����˶��κ����ۺ��Լ����ε��ж��������Լ����ɶ�����֪ʶ���������ν�ϵó�F��λ���ǽ���ؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�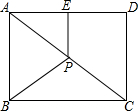 ��ͼ��P�Ǿ���ABCD�ĶԽ���AC���е㣬E��AD���е㣮��AB=6��AD=8�����ı���ABPE���ܳ�Ϊ��������
��ͼ��P�Ǿ���ABCD�ĶԽ���AC���е㣬E��AD���е㣮��AB=6��AD=8�����ı���ABPE���ܳ�Ϊ��������| A�� | 14 | B�� | 16 | C�� | 17 | D�� | 18 |
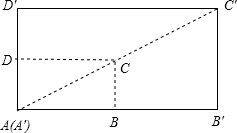 ��ͼ������ABCD�����A��B��C��D����λ��ͼ�Σ�A��λ�����ģ���֪����ABCD���ܳ�Ϊ24��BB��=4��DD��=2����AB��AD�ij���
��ͼ������ABCD�����A��B��C��D����λ��ͼ�Σ�A��λ�����ģ���֪����ABCD���ܳ�Ϊ24��BB��=4��DD��=2����AB��AD�ij���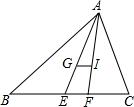 �ڡ�ABC�У�BC=a��CA=b��AB=c��G��I�ֱ��ǡ�ABC�����ĺ����ģ���GI��BC�����ҳ�a��b��c֮���������ϵ����֤����Ľ��ۣ�
�ڡ�ABC�У�BC=a��CA=b��AB=c��G��I�ֱ��ǡ�ABC�����ĺ����ģ���GI��BC�����ҳ�a��b��c֮���������ϵ����֤����Ľ��ۣ� �ı���ABCDΪ���Σ���ͼ��ʾ������AD��BC��OΪһ���е㣮
�ı���ABCDΪ���Σ���ͼ��ʾ������AD��BC��OΪһ���е㣮 ��ͼ���ڱ߳�Ϊ2��������ABCD�У��ֱ��Ը�����ΪԲ�ģ�����������������Բ����ʹ�������ڵ�Բ�����ڵ�E��F��G��H����ͼ����Ӱ���ֵ���Χ���ܳ���2�У�����������У�
��ͼ���ڱ߳�Ϊ2��������ABCD�У��ֱ��Ը�����ΪԲ�ģ�����������������Բ����ʹ�������ڵ�Բ�����ڵ�E��F��G��H����ͼ����Ӱ���ֵ���Χ���ܳ���2�У�����������У�