题目内容
7.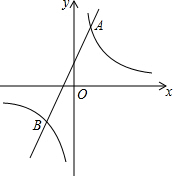 已知反比例函数y=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
已知反比例函数y=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).(1)求这两个函数的表达式;
(2)观察图象,当x>0时,直接写出y1>y2时自变量x的取值范围.
分析 (1)由点A的坐标,利用反比例函数图象上点的坐标特征,即可求出反比例函数表达式,由点B的纵坐标结合反比例函数图象上点的坐标特征,即可求出点B的坐标,根据点A、B的坐标利用待定系数法,即可求出一次函数表达式;
(2)根据两函数图象的上下位置关系,即可找出当x>0时,y1>y2的自变量x的取值范围
解答 解:(1)∵反比例函数y1=$\frac{k}{x}$的图象经过点A﹙1,4﹚,
∴k=1×4=4,
∴反比例函数的表达式为y1=$\frac{4}{x}$.
∵点B﹙m,-2﹚在反比例函数的图象上,
∴m=$\frac{4}{-2}$=-2,
∴点B的坐标为(-2,-2).
∵一次函数的图象经过点A、B,将这两个点的坐标代入y2=ax+b,
得$\left\{\begin{array}{l}a+b=4\\-2a+b=-2\end{array}\right.$,解得:$\left\{\begin{array}{l}a=2\\ b=2\end{array}\right.$,
∴一次函数的表达式为y2=2x+2.
(2)观察函数图象可知:当x<-2或0<x<1时,反比例函数图象在一次函数图象上方,
∴当x>0时,y1>y2的自变量x的取值范围为0<x<1.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及待定系数法求一次函数解析式,解题的关键是:(1)利用待定系数法求出函数表达式;(2)根据两函数图象的上下位置关系,找出不等式的解集.

练习册系列答案
相关题目
18.小明统计了他家今年3月份打电话的次数及通话时间,并列出了频数分布表:
则通话时间不超过10min的频率为( )
| 通话时间x/min | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
| 频数(通话次数) | 20 | 15 | 9 | 6 |
| A. | 0.1 | B. | 0.3 | C. | 0.5 | D. | 0.7 |
15.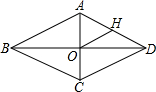 如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )
如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )
 如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )
如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
12.在3.14、$\sqrt{12}$、$\frac{22}{7}$、$-\sqrt{5}$、$\root{3}{27}$、2π、0.2020020002这六个数中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.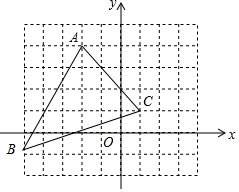 如图,若将△ABC先向右平移5个单位长度(1格代表1个单位长度),再向下平移3个单位长度得到△A1B1C1,则点A的对应点A1的坐标是( )
如图,若将△ABC先向右平移5个单位长度(1格代表1个单位长度),再向下平移3个单位长度得到△A1B1C1,则点A的对应点A1的坐标是( )
 如图,若将△ABC先向右平移5个单位长度(1格代表1个单位长度),再向下平移3个单位长度得到△A1B1C1,则点A的对应点A1的坐标是( )
如图,若将△ABC先向右平移5个单位长度(1格代表1个单位长度),再向下平移3个单位长度得到△A1B1C1,则点A的对应点A1的坐标是( )| A. | (3,1) | B. | (9,-4) | C. | (-6,7) | D. | (-1,2) |
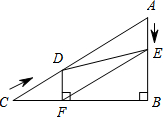 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts(0<t≤15).过点DDF⊥BC于点F,连接DE,EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts(0<t≤15).过点DDF⊥BC于点F,连接DE,EF.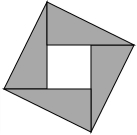 2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )