Question

7．在△ABC中，AD为BC边上的中线，
（1）如图1，求证：AB+AC＞2AD；
（2）如图2，若∠BAC＜90°，作EA⊥AC，FA⊥BA，且AE=AC，AF=AB，连接EF，写出AD与EF的数量关系，并证明．

Answer 1

分析 （1）延长AD至E，使DE=AD，连接CE，证明△CDE与△ADB全等，再利用三角形的三边关系证明即可；
（2）延长AD到M，使AD=DM，连接BM、CM，根据∠ABM+∠BAC=180°、∠EAC+∠BAF=180°知∠ABM=∠EAF，再证△AEF≌△BMA可得．

解答 证明：（1）如图1，延长AD至E，使DE=AD，连接CE，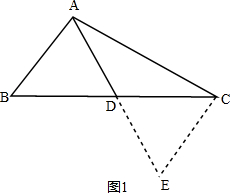

在△CDE与△ADB中
$\left\{\begin{array}{l}{AD=DE}\\{∠ADB=∠EDC}\\{BD=CD}\end{array}\right.$，
∴△CDE≌△ADB（SAS），
∴AB=CE，
∴AC+CE=AC+AB＞AE=2AD，
即AC+AB＞2AD；
（2）EF=2AD，
如图2，延长AD到M，使AD=DM，连接BM、CM，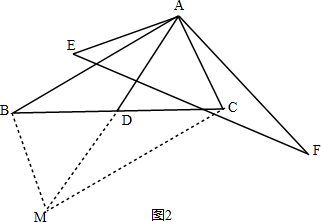

∵BD=DC，AD=DM，
∴四边形ABMC是平行四边形，
∴AC=BM=AE，BM∥AC，
∴∠ABM+∠BAC=180°，
又∵EA⊥AC，FA⊥BA，
∴∠EAC+∠BAF=90°+90°=180°，即∠EAF+∠BAC=180°，
∴∠ABM=∠EAF，
在△AEF和△BMA中，
∵$\left\{\begin{array}{l}{AE=BM}\\{∠EAF=∠MBA}\\{AF=AB}\end{array}\right.$，
∴△AEF≌△BMA（SAS），
∴EF=AM=2AD．

点评 本题主要考查全等三角形的判定和性质，添加辅助线构建全等三角形将待证线段利用全等三角形联系到一起是关键．