题目内容
10．下列长度的各组线段首尾相接能构成的三角形的是（ ）| A． | 2cm、3cm、5cm | B． | 3cm、5cm、6cm | C． | 2cm、2cm、4cm | D． | 3cm、5cm、10cm |
分析 三角形三边关系：三角形任意两边之和大于第三边，据此判断即可．
解答 解：（A）∵2+3=5，∴2cm、3cm、5cm首尾相接不能构成的三角形；
（B）∵3+5＞6，∴3cm、5cm、6cm首尾相接能构成的三角形；
（C）∵2+2=4，∴2cm、2cm、4cm首尾相接不能构成的三角形；
（D）∵3+5＜10，∴3cm、5cm、10cm首尾相接不能构成的三角形．
故选（B）
点评 本题主要考查了三角形的三边关系，在运用三角形三边关系判定三条线段能否构成三角形时，并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度，即可判定这三条线段能构成一个三角形．
练习册系列答案
相关题目
20．若方程组$\left\{\begin{array}{l}{x+y=☆}\\{2x+y=16}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=6}\\{y=□}\end{array}\right.$，则被“☆”、“□”遮住的两个数分别是（ ）
| A． | 10，3 | B． | 3，10 | C． | 4，10 | D． | 10，4 |
18．
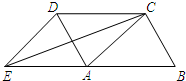已知：如图，四边形ABCD是平行四边形，延长BA到点E，使AE=AB，联结ED、EC、AC．添加一个条件，能使四边形ACDE成为矩形的是（ ）
已知：如图，四边形ABCD是平行四边形，延长BA到点E，使AE=AB，联结ED、EC、AC．添加一个条件，能使四边形ACDE成为矩形的是（ ）| A． | AC=CD | B． | AB=AD | C． | AD=AE | D． | BC=CE． |
5．
如图，在?ABCD 中，已知 AE、CF 分别是∠DAB、∠BCD 的角平分线，则下列说法正确的是（ ）
如图，在?ABCD 中，已知 AE、CF 分别是∠DAB、∠BCD 的角平分线，则下列说法正确的是（ ）| A． | 四边形AFCE是平行四边形 | B． | 四边形AFCE是菱形 | ||
| C． | 四边形ABCF是等腰梯形 | D． | 四边形AECD是等腰梯形 |
15．下列长度的三条线段能组成三角形的是（ ）
| A． | 1.5cm，2cm，2.5cm | B． | 2cm，5cm，8cm | C． | 1cm，3cm，4cm | D． | 5cm，3cm，1cm |
2．下列命题不正确的是（ ）
| A． | 两直线平行，同位角相等 | |
| B． | 两点之间直线最短 | |
| C． | 对顶角相等 | |
| D． | 从直线外一点到直线上的所有线段中，垂线段最短 |
19．下列命题是假命题的是（ ）
| A． | 三角形的三条角平分线相交于一点，并且这一点到三边距离相等 | |
| B． | 等腰三角形底边的中点到两腰的距离相等 | |
| C． | 面积相等的两个三角形全等 | |
| D． | 一个三角形中至少有两个锐角 |