题目内容
20.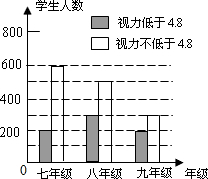 某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图如图所示,则下列说法中不正确的是( )
某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图如图所示,则下列说法中不正确的是( )| A. | 本次抽查活动共抽查了2100名学生 | |
| B. | 本次抽查活动中视力不低于4.8的学生人数占总人数的66.7% | |
| C. | 本次抽查活动中视力不低于4.8学生人数中的极差为300人 | |
| D. | 由活动结果可以知道随着年级的增长,视力低于4.8的人数越来越多,呈上升趋势,那么同年级中抽到视力不低于4.8的学生的概率将越来越小 |
分析 利用各部分的和等于总体求出抽查的学生总数,即可判断A;
用视力不低于4.8的学生人数除以总人数,即可判断B;
根据极差的定义,用视力不低于4.8的学生人数的最大值减去最小值,即可判断C;
根据条形统计图可知,视力低于4.8的人数七年级与九年级都是200人,八年级为300人,由此即可判断D.
解答 解:A、∵200+600+300+500+200+300=2100,
∴本次抽查活动中共抽查了2100名学生,故说法正确;
B、∵600+500+300=1400,
∴本抽查中视力不低于4.8的学生人数为1400人,
∵1400÷2100=$\frac{2}{3}$≈66.7%,
∴本次抽查活动中视力不低于4.8的学生人数约占总人数的66.7%,故说法正确;
C、本次抽查活动中视力不低于4.8学生人数中的极差为:600-300=300人,故说法正确;
D、由活动结果可以知道,视力低于4.8的人数七年级为200人,八年级为300人,九年级为200人,所以视力低于4.8的人数不是越来越多,没有呈上升趋势,同年级中抽到视力不低于4.8的学生的概率也不是越来越小,故说法错误.
故选D.
点评 本题考查的是条形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.也考查了极差的定义与概率公式.

练习册系列答案
相关题目
10.下列运算错误的是( )
| A. | (-a)(-a)2=-a3 | B. | -2x2(-3x)=-6x4 | C. | (-a)3(-a)2=-a5 | D. | (-a)3(-a)3=a6 |
15.计算3y3•(-y2)2•(-2y)3的结果是( )
| A. | -24y10 | B. | -6y10 | C. | -18y10 | D. | 54y10 |
5.正八边形的中心角是( )
| A. | 45° | B. | 135° | C. | 360° | D. | 1080° |
12.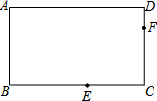 在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F.若AD=$\sqrt{3}$AB=$\sqrt{3}$,则AF2=( )
在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F.若AD=$\sqrt{3}$AB=$\sqrt{3}$,则AF2=( )
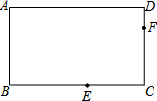 在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F.若AD=$\sqrt{3}$AB=$\sqrt{3}$,则AF2=( )
在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F.若AD=$\sqrt{3}$AB=$\sqrt{3}$,则AF2=( )| A. | 8-4$\sqrt{3}$ | B. | 10-4$\sqrt{3}$ | C. | 8+4$\sqrt{3}$ | D. | 10+4$\sqrt{3}$ |
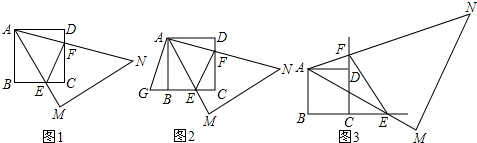
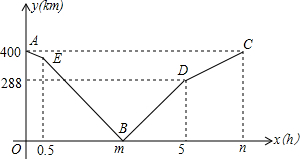 甲乙两地相距400km,一辆轿车从甲地出发,以一定的速度匀速驶往乙地.0.5h后,一辆货车从乙地出发匀速驶往甲地(轿车的速度大于货车的速度),与轿车在途中相遇.此后,两车继续行驶,并各自到达目的地.两车之间的距离y(km)与轿车行驶的时间x(h)的函数图象如图.
甲乙两地相距400km,一辆轿车从甲地出发,以一定的速度匀速驶往乙地.0.5h后,一辆货车从乙地出发匀速驶往甲地(轿车的速度大于货车的速度),与轿车在途中相遇.此后,两车继续行驶,并各自到达目的地.两车之间的距离y(km)与轿车行驶的时间x(h)的函数图象如图.